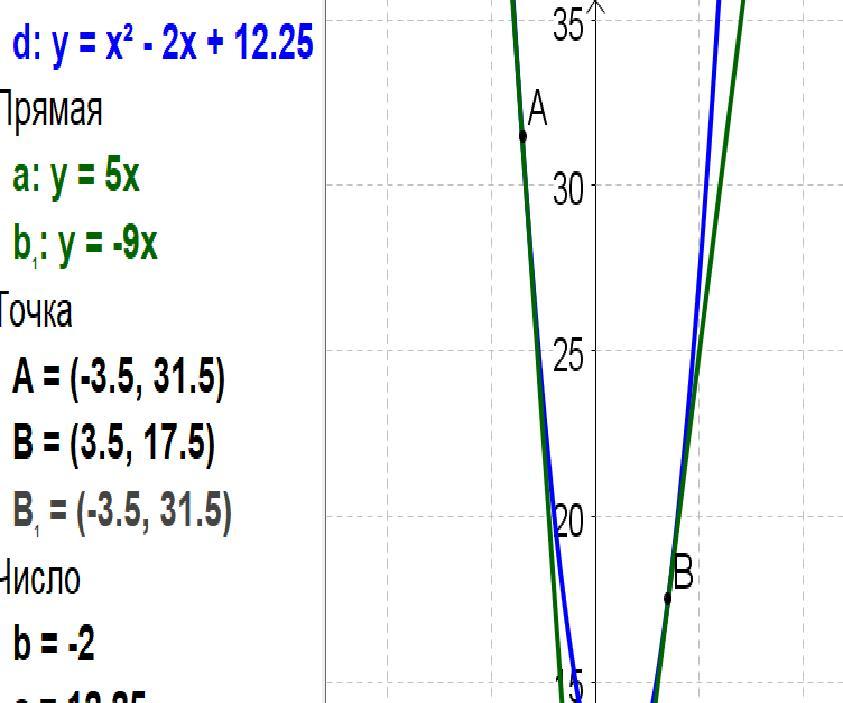
При каких значениях b и с прямые y=5x и y=-9x являются касательными к графику функции F(X)=x^2+bx+c?
b=_;
c=_;
Заранее спасибо

Ответы
3. При каких b и c прямые y = 5x и y = – 9x являются касательными к графику функции y = x2 + bx + c?
Решение.
Пусть t – абсцисса точки касания прямой y = 5x с параболой y = x2 + bx + c; p – абсцисса точки касания прямой y = – 9x с параболой y = x2 + bx + c.
Составим и решим 2 системы уравнений, связывающих параболу и 2 касательные.
Уравнение касательной к параболе в общем виде выглядит так:
Но так как коэффициент а равен 1, то уравнение касательной y = 5x примет вид y = (2t + b)x + c – t2, а уравнение касательной y = – 9x примет вид y = (2p + b)x + c – p2.
{2t + b = 5 {2p + b =-9
{c - t² = 0 {c - p² = 0. Отсюда видим, что t² = p².
Так как касание происходит в ветвях параболы с разных сторон её вертикальной оси, то t = -p.
Сложим 2 первых уравнения с учётом, что t = -p.
2*(-p) + b = 5
2p + b =-9
2b = -4, b = -4/2 = -2.
Отсюда определяем t = (5 – b)/2 = (5 – (-2))/2 = 7/2 = 3,5.
p = (-9 – b)/2 = (-9 – (-2))/2 = -7/2 = -3,5.
Параметр с = t² = 3,5² = 12,25.
Ответ: уравнение параболы y = x² - 2x + 12,25.