Предмет: Алгебра,
автор: vladreznicenko830
5. Обчисліть
6. Знайдіть значення виразу
Приложения:
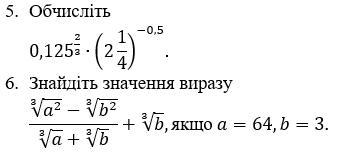
Ответы
Автор ответа:
1
Ответ:
Применяем правила действий со степенями .
Похожие вопросы
Предмет: Алгебра,
автор: pankratovalilia3
Предмет: Українська література,
автор: trrnuxjrb
Предмет: Литература,
автор: barimbekovilias
Предмет: Математика,
автор: fatima9842887
Предмет: Физкультура и спорт,
автор: ikislenkova74