Помогите пожалуйста по алгебре
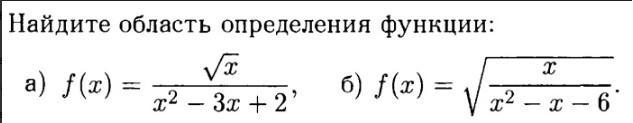
Ответы
Ответ:
Объяснение:
а) f(x) = √x / (x² - 3x + 2)
1. Рассмотрим сначала функцию:
f₁(x) = √x - подкоренное выражение должно быть ≥0, т.е. x≥0
D(f₁): x ∈ [0; +∞)
2. f₂ (x) = x² - 3x + 2 - это знаменатель, он не может = 0
x² - 3x + 2 ≠ 0
x² - x - 2x + 2≠ 0
x(x - 1) -2(x - 1) ≠ 0
(x - 1)(x - 2) ≠ 0
x₁ ≠ 1, x₂ ≠2
Ответ: D(f): x ∈ [0; 1)∪(1; 2) ∪(2; + ∞)
б)
f(x) = √[x/(x² - x - 6)]
1. f₁(x) = x² - x - 6
x² - x - 6 ≠ 0
Найдем корни уравнения: x² - x - 6 = 0
x² + 2x - 3x - 6 = 0
x(x + 2) -3(x + 2) = 0
(x + 2)(x - 3) = 0
x₁ = -2; x₂ = 3
D(f₁): x ∈ (-∞; -2) ∪ (-2; 3) ∪(3; + ∞)
2. Подкоренное выражение должно быть ≥0:
x/(x² - x - 6) ≥ 0
---------- -2--------0-------- 3---------
1) x < - 2 → например, x = -3 → (-3)/(9+3-6) < 0 - не подходит
2) -2< x < 0 → пусть x = -1 → (-1)/(1+1-6) = -1/-4 > 0 - удовлетворяет условию;
3) x = 0 → f(0) = 0 - удовлетворяет
3) 0 <x < 3 → x = 1 → 1/(1-1-6) < 0 - не подходит
4) x > 3 → x = 4 → 4/(16 - 4 - 6) > 0
Ответ: D(f): x ∈(- 2;0] ∪ (3; + ∞)