Предмет: Геометрия,
автор: ilonaolejnik720
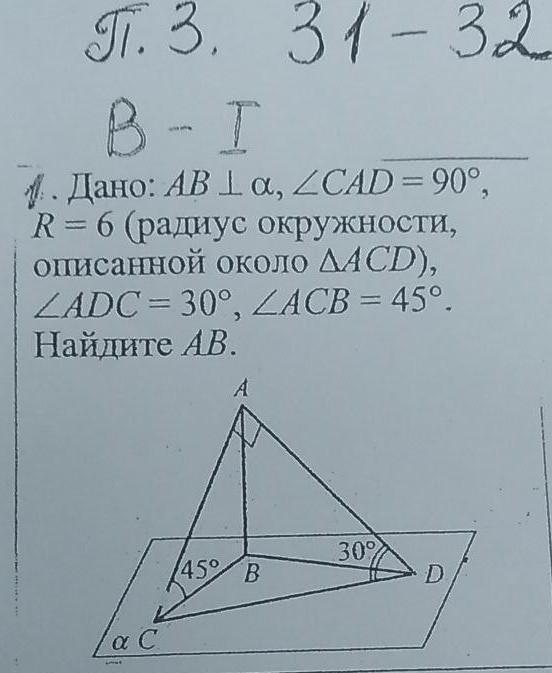
Дано: AB La, ZCAD = 90°, R = 6 (радиус окружности, описанной около ДАСD), ZADC-30°, ZACB = 45°. Найдите АВ.
Приложения:
Ответы
Автор ответа:
2
Ответ:
Ответ: 8/√3 (ед.длины)
Объяснение: АВ перпендикулярно плоскости альфа ⇒АВ перпендикулярно любой прямой, лежащей в этой плоскости ⇒ АВ⊥АС и АВ⊥АD.
Треугольники АВС и ∆АВD имеют по равному острому углу (дано) и общему катету АВ, следовательно, они равны. из чего следует равенство катетов прямоугольного ∆ АСD, т.е. АС=АD и углы АСD=ADC=(180°-90°):2=45°.
Центром окружности, описанной около прямоугольного треугольника, является середина его гипотенузы. R=CO=DO=4√2. ⇒ медиана АО=R=4√2, а
АС=СО/sin45°=4√2)/√3/2=8 (ед. длины)
Из прямоугольного ∆ АВС катет АВ=АС•tg30°=8•1/√3=8/√3
Похожие вопросы
Предмет: Литература,
автор: darapledzian
Предмет: Физика,
автор: witchk6446
Предмет: Математика,
автор: busyy2012
Предмет: Українська мова,
автор: katushhhsa
Предмет: Английский язык,
автор: lizaklein69