Предмет: Геометрия,
автор: syhqvvw
СРОЧНО!!!! 40 БАЛОВ
Знайдіть площу основи та площу бічної поверхні правильної n-кутної піраміди, якщо n=3 радіус кола описаного навколо основи дорівнює R, а бічна грань утворює з основновою кут бета
Ответы
Автор ответа:
1
Ответ:
Sбок = 3√3 * R^2 * cosβ/2
Sосн = 3√3R^2/4
Объяснение:
Sбок = 0.5* Pосн *d
SN = d
R = a * √3/3
AO = R; AB = R√3 ; AN = AB/2 = R√3 : 2 =>
NO^2 = R^2 - (R√3 : 2)^2 = 4R^2/4 - 3R^2/4 = R^2/4
NO = R/2
SN = NO/cosβ = Rcosβ/2
Pосн = AB*3 = 3R√3
Sбок = Rcosβ/2 * 3R√3 * 0.5 = 3√3 * R^2 * cosβ/2
Sосн = √3/4 * AB^2 = 3R^2*√3/4 = 3√3R^2/4
Приложения:
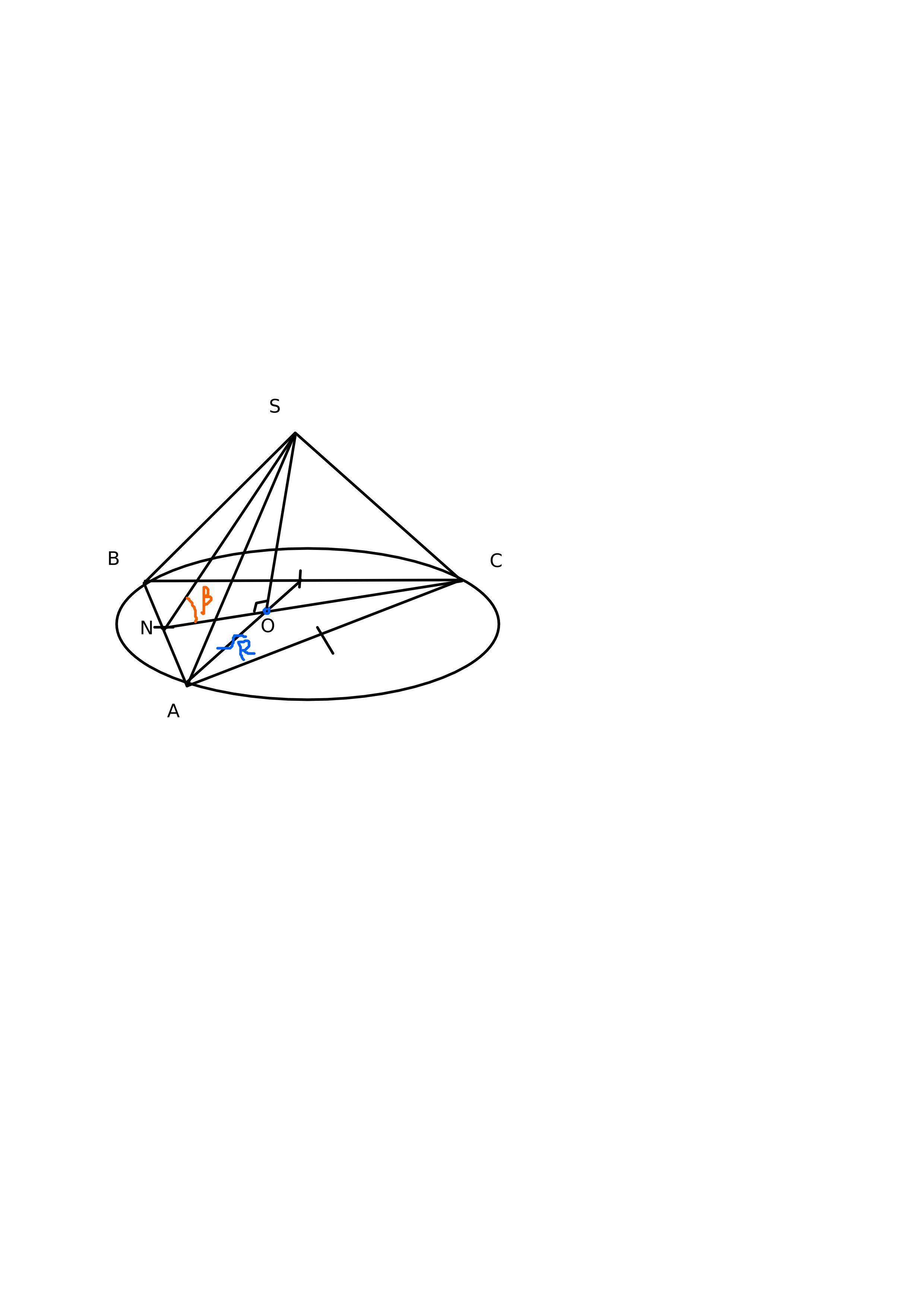
antvsemizvestniy:
забыл рисунок добавить
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Биология,
автор: ostapp2474
Предмет: Английский язык,
автор: veronichkarotar
Предмет: Литература,
автор: kovalchukvi2005
Предмет: Алгебра,
автор: rhfcysqubufyn