Question

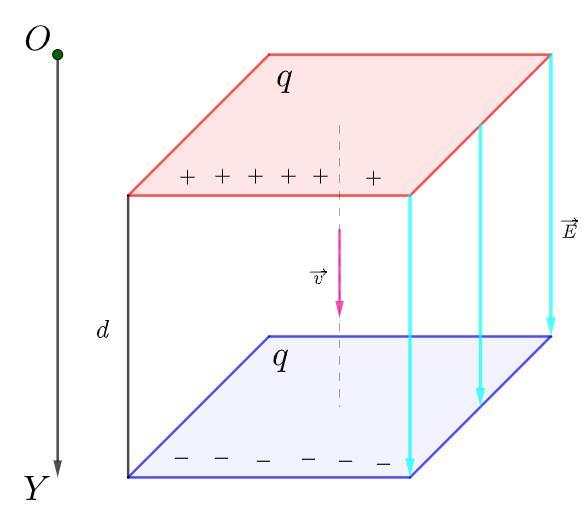
Плоский повітряний конденсатор з площею пластин 120 см² і відстанню між ними 8 мм запяджено і вимкнуто із джерела. Протон, переміщуючись під дією сил поля від однієї обкладинки до іншої, матиме швидкість 8*10⁶ м/с. Знайти заряд на обкладинках конденсатора. ​​

Answer 1

Ответ:

Заряд на обкладках конденсатора равен 443,385 · 10⁻⁸ Кл

Примечание:

Предполагаем, что начальная скорость протона 0 м/, а конечная скорость 8 · 10⁶ м/с

Объяснение:

Дано:

$S =$ 0,012 м²

$d =$ 0,008 м

$\xi =$ 1

$\xi =$ 8,85 · 10⁻¹² Ф/м

$v_{0} =$ 0 м/с

$v =$ 8 · 10⁶ м/с

$q_{p} =$ 1,6 · 10⁻¹⁹ Кл

$m_{p} =$ 1,67 · 10⁻²⁷ кг

Найти:

$q \ - \ ?$

-----------------------------------

Решение:

Модуль силы действующий на протон со стороны электрического поля:

$F_{e} = q_{p}E$

По формуле (в скалярной форме):

$v^{2} - v_{0}^{2} = 2ad$, так как по условию 0 м/с, то:

$v^{2} = 2ad \Longrightarrow a = \dfrac{v^{2}}{2d}$

По следствию из второго закона Ньютона:

$F_{e} = m_{p}a$

$q_{p}E = m_{p}a$

$q_{p}E = \dfrac{m_{p}v^{2}}{2d} \Longrightarrow \boxed{ E = \dfrac{m_{p}v^{2}}{2q_{p}d} }$ - напряженность электрического поля

Ёмкость плоского конденсатора:

$C= \dfrac{\xi \xi_{0}S}{d}$

Максимальное напряжение конденсатора:

$U = Ed$

Заряд конденсатора:

$q = CU = \dfrac{\xi \xi_{0}S Ed}{d} = \xi \xi_{0}S E = \dfrac{S\xi \xi_{0}m_{p}v^{2}}{2q_{p}d}$

$\boldsymbol{\boxed{q = \dfrac{S\xi \xi_{0}m_{p}v^{2}}{2q_{p}d}}}$ - заряд на обкладках конденсатора

Расчеты:

$\boldsymbol q =$ (0,012 м²· 1 · 8,85 · 10⁻¹² Ф/м · 1,67 · 10⁻²⁷ кг · 64 · 10¹² м/с) /

/ (2 · 1,6 · 10⁻¹⁹ Кл · 0,008 м) = 443,385 · 10⁻⁸ Кл

Ответ: $q =$ 443,385 · 10⁻⁸ Кл.