Question

Помогите пожалуйста простой вопрос!
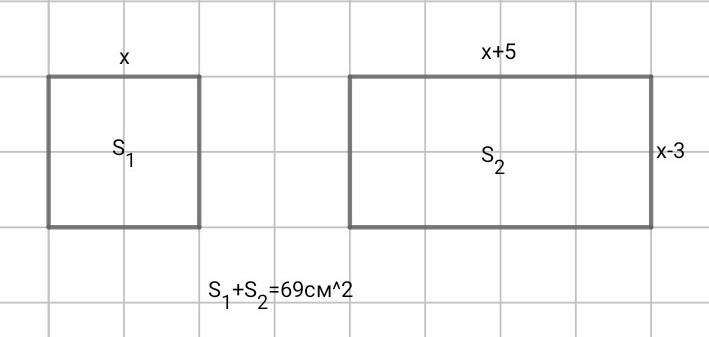
Даны квадрат и прямоугольник. Сторона квадрата на 5 см меньше одной из сторон прямоугольника и на 3 см больше другой его стороны. Известно, что сумма площадей фигур 69 см^2.
Найдите площадь квадрата.
Найдите площадь прямоугольника.

Answer 1

Ответ:

х- сторона квадрата;

х+5блльшая сторона прямоугольника

х-3 меньшая сторона прямоугольника

(х+5)(х-3) - площадь прямоугольника

х2- площадь квадрата

Составим уравнение: х²+(х+5)(х-3)=69

х²+х²-3х+5х-15=69; 2х²+2х-84=0; х²+х-42=0;

D=1+168=169; x1=(-1-13)/2=-7;x2=(-1+13)/2=6;x²=36;

(6+5)(6-3)=11•3=33

Ответ: площадь квадрата 36 см²;

площадь прямоугольника- 33см²

Answer 2

Ответ:

Площадь квадрата равна 36(см)²

Площадь прямоугольника равна 33(см)²

Объяснение:

Если сторона квадрата на 5см меньше , то одна из сторон прямоугольника будет на 5см больше.

Если сторона квадрата на 3см больше , то одна из сторон прямоугольника будет на 3см меньше

Тогда сторона квадрата пусть будет: x , а длина прямоугольника: x+5 , ширина: x-3.

Площадь квадрата : S₁ , площадь прямоугольника : S₂.

S₁ = x² ; S₂ = (x+5)(x-3)

По условию сумма площадей равна 69(см)²

$x {}^{2} + (x + 5)(x - 3) = 69 \\ x {}^{2} + x {}^{2} - 3x + 5x - 15 - 69 = 0 \\ 2x {}^{2} + 2x - 84 = 0|:2 \\ x {}^{2} + x - 42 = 0$

Данное квадратное уравнение решим через дискриминант:

$D = 1 {}^{2} - 4 \cdot( - 42) = 1 + 168 = 169$

$\displaystyle x_{1,2} = \frac{ - 1 \pm \sqrt{169} }{2} = \frac{ - 1 \pm13}{2} \\ \Rightarrow x_1 = 6 \: \: \: \: \: x_2 = - 7$

Отрицательный корень исключается , т.к сторона фигур может быть только положительной.

Вернёмся к площадям фигур:

S₁ = x² = 6² = 36(см)²

S₂ = (x+5)(x-3) = (6+5)(6-3) = 11 · 3 = 33(см)²