Предмет: Алгебра,
автор: naomy2
Доведіть , що значення виразу є раціональним числом
Приложения:
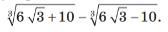
Ответы
Автор ответа:
2
Ответ:
Обозначим заданное выражение буквой А .
Возведём это выражение в куб, применив формулу
.
Получим
Получили равенство: .
Это кубическое уравнение легко решить , так как корень находится подбором. При подстановке значения А=2 в равенство получаем 0. Значит левая часть равенства делится нацело на разность (А-2) .
Квадратный трёхчлен действительных корней не имеет , так как его дискриминант отрицательный:
. Поэтому далее разложение на множители невозможно .
Получили, что - действительное число, оно является и рациональным тоже .
olyaostapenkokr:
Здрастуйте, а нельзя ли было остановиться на нахождении А подбором, или нужно обязательно рассмотреть делимось равенства на (А-2)?
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Французский язык,
автор: lambaposhtaruk
Предмет: Українська мова,
автор: larenm445
Предмет: Физкультура и спорт,
автор: arina20071115
Предмет: Математика,
автор: olgakoczur