Предмет: Алгебра,
автор: be3yh4ikgg
БУДЬ ЛАСКА! Поясніть як, без Photomath, там ну зовсім не так як у класі! У мене лише 2 гарні оцінки, будь-ласка допоможіть.
Приложения:

Ответы
Автор ответа:
1
Ответ:
решение смотри на фотографии
Приложения:
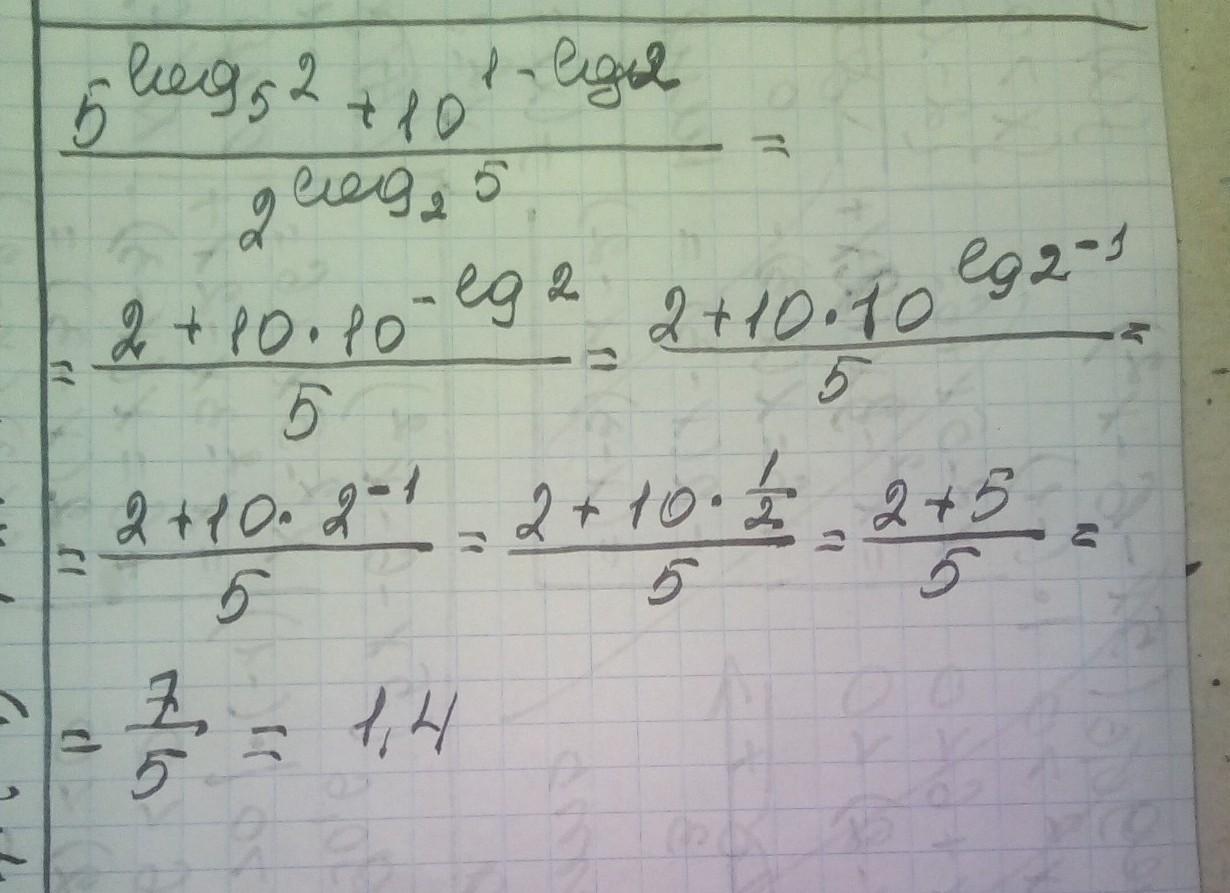
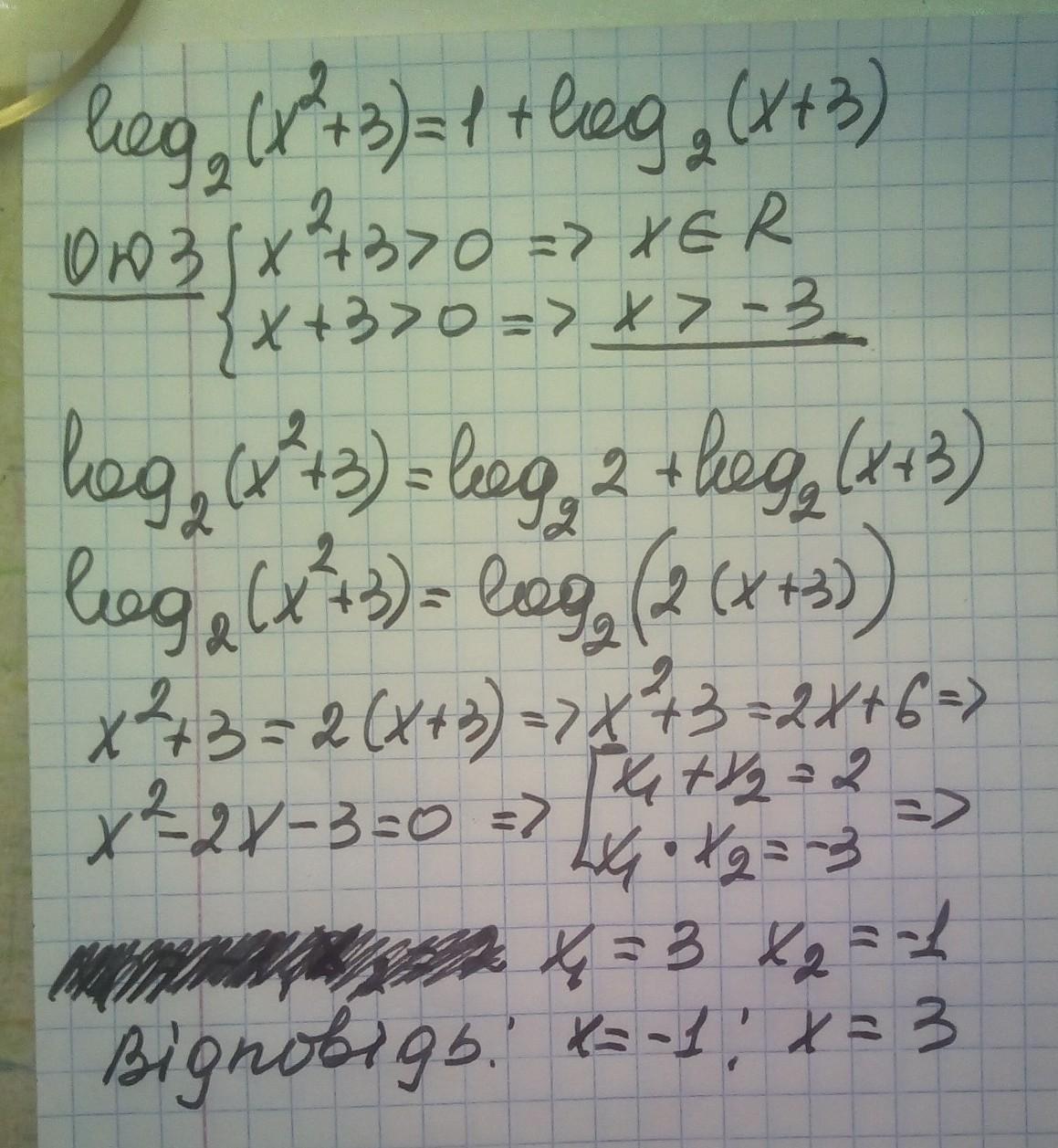
Автор ответа:
0
asdjkasdajksdjka:
помогите пожалуйста срочно!
умоляю
https://znanija.com/task/50614125
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Қазақ тiлi,
автор: amikaasika
Предмет: Английский язык,
автор: ami1070
Предмет: Математика,
автор: lori55565