Question

ПОМОГИТЕ ПОЖАЛУЙСТА ДАЮ 100 БАЛЛОВ!!!

Пробкова кулька радіусом 5 мм спливає в посудині наповненій касторовим маслом. Чому дорівнює динамічна та кінематична в’язкості касторового масла в умовах досліду, якщо кулька спливає з сталою швидкістю 3,5 с?

Answer 1

Ответ:

Динамическая вязкость равна приблизительно 0,012 Па · с, а кинематическая вязкость равна приблизительно 1,3 · 10⁻⁵ м²/c

Примечание:

Плотность пробки может лежать в диапазоне от 120 кг/м³ до

240 кг/м³ в зависимости от состава.

Считаем, что "3,5 с", значит 3,5 м/c

Число Рейнольдса для данного шарика будет крайне малым

Объяснение:

Дано:

$R =$ 0,005 м

$\rho_{p} =$ 200 кг/м³

$\rho_{m} =$ 960 кг/м³

$v =$ 3,5 м/c

$g =$ 10 м/c²

Найти:

$\eta \ - \ ?$

$\nu \ - \ ?$

----------------------------------------

Решение:

Объем шарика:

$V = \dfrac{4}{3} \pi R^{3}$

Масса шарика через его плотность:

$m = \rho_{p}V = \dfrac{4}{3} \pi \rho_{p} R^{3}$

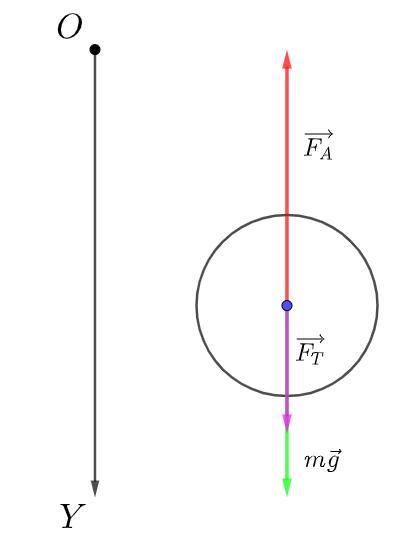
Модуль силы Архимеда:

$F_{A} = \rho_{m}g V = \dfrac{4}{3}\rho_{m} \pi g R^{3}$

Модуль силы Стокса:

$F_{T} = 6 \pi R \eta v$

Так как шарик всплывает равномерно, то по законам статики сумма всех сил действующих на тело равна нулю:

$\overrightarrow{F_{A}} + \overrightarrow{F_{T}} + m \vec{g} = 0$

$OY: -F_{A} + F_{T} + mg = 0 \Longrightarrow F_{A} = F_{T} + mg$

$\dfrac{4}{3}\rho_{m} \pi g R^{3} =6 \pi R \eta v+ \dfrac{4}{3} \pi \rho_{p} g R^{3}$

$6 \pi R \eta v = \dfrac{4}{3}\rho_{m} \pi g R^{3} - \dfrac{4}{3} \pi \rho_{p} g R^{3} = \dfrac{4}{3} \pi g R^{3} \bigg (\rho_{m} - \rho_{p} \bigg) \Longrightarrow \eta = \dfrac{\dfrac{4}{3} \pi g R^{3} \bigg (\rho_{m} - \rho_{p} \bigg)}{6 \pi R v} =$

$= \dfrac{\dfrac{4}{3} g R^{2} \bigg (\rho_{m} - \rho_{p} \bigg)}{6v} = \dfrac{4 g R^{2} \bigg (\rho_{m} - \rho_{p} \bigg)}{18v} = \dfrac{2 g R^{2} \bigg (\rho_{m} - \rho_{p} \bigg)}{9v}$

$\boldsymbol{\boxed{\eta = \dfrac{2 g R^{2} \bigg (\rho_{m} - \rho_{p} \bigg)}{9v} }}$ - динамическая вязкость

Кинематическая вязкость:

$\nu= \dfrac{\eta}{\rho_{m}} = \dfrac{\dfrac{2 g R^{2} \bigg (\rho_{m} - \rho_{p} \bigg)}{9v}}{\dfrac{\rho_{m}}{1} } = \dfrac{2 g R^{2} \bigg (\rho_{m} - \rho_{p} \bigg)}{9v \rho_{m}}$

$\boldsymbol{\boxed{\nu = \dfrac{2 g R^{2} \bigg (\rho_{m} - \rho_{p} \bigg)}{9v \rho_{m}} }}$ - кинематическая вязкость

Расчеты:

$\boldsymbol \eta =$ (2 · 10 м/c² · 0,000025 м²(960 кг/м³ - 200 кг/м³)) / (9 · 3,5 м/c) $\boldsymbol \approx$

$\boldsymbol \approx$ 0,012 Па · с.

$\boldsymbol \nu =$ (2 · 10 м/c² · 0,000025 м²(960 кг/м³ - 200 кг/м³)) / (9 · 3,5 м/c ·

· 960 кг/м³) $\boldsymbol \approx$ 1,3 · 10⁻⁵ м²/c

Ответ: $\eta \approx$ 0,012 Па · с. $\nu \approx$ 1,3 · 10⁻⁵ м²/c.