Предмет: Алгебра,
автор: spamgg002
Изобразить на числовой прямой несколько членов последо вательности {Xn} и выяснить, к какому числу они прибли жаются:
1) Xn = 1/n ;
2)Xn = (-1)^n/n ;
3) Xn =n+1/n ;
нужно ОБЪЯСНИТЬ КАК РЕШАТЬ и решить подробно (желательно на листе)
Приложения:
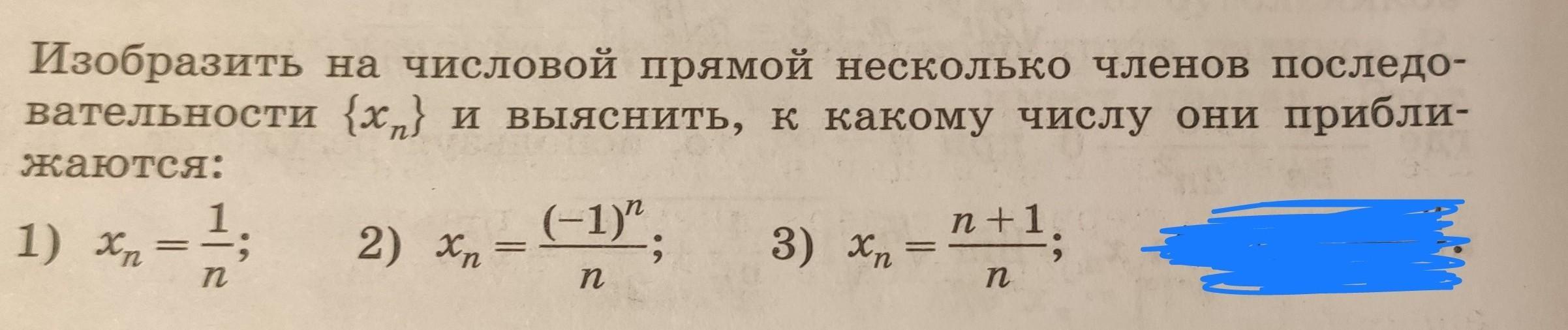
Ответы
Автор ответа:
1
Ответ:
1) Изобразим несколько членов последовательности
При неизменном числителе и увеличении знаменателя дробь будет уменьшаться . Значения членов последовательности будут приближаться к 0 , оставаясь немного больше 0 .
при
.
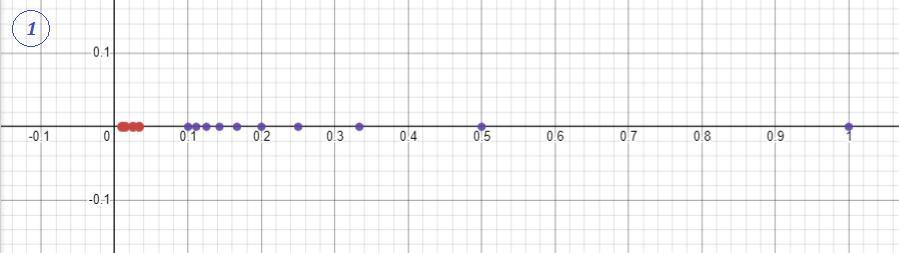
2) Изобразим несколько членов последовательности
Члены последовательности чередуют знаки, то плюс, то минус . Но всё равно значения членов последовательности приближаются к числу 0 , то слева, то справа , при
.
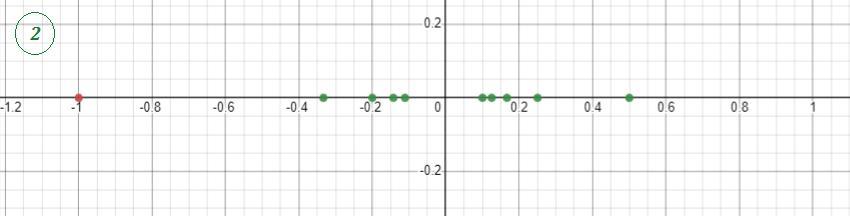
3) Изобразим несколько членов последовательности
Значения членов последовательности будут приближаться к 1 , оставаясь немного больше 1 .
при
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: fasrey31
Предмет: Английский язык,
автор: revtgalina8
Предмет: Алгебра,
автор: polapalo123
Предмет: Немецкий язык,
автор: igormalitskii3
Предмет: История,
автор: alinacordero2005