Предмет: Алгебра,
автор: dbatauzov97597
помогите решить даю 100б
Приложения:
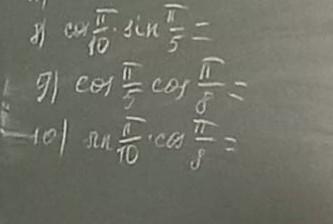
Ответы
Автор ответа:
1
Ответ:
Применяем формулы произведений тригонометрических функций sin на cos , cos на cos .
NNNLLL54:
перезвгрузи страница
Похожие вопросы
Предмет: Українська мова,
автор: udav4ik987
Предмет: Английский язык,
автор: zlataskozub27
Предмет: Физика,
автор: elizabetpiu205
Предмет: Литература,
автор: foks081017
Предмет: Математика,
автор: solomiiafunny