Предмет: Алгебра,
автор: korrzh
Найти значение выражения
Приложения:
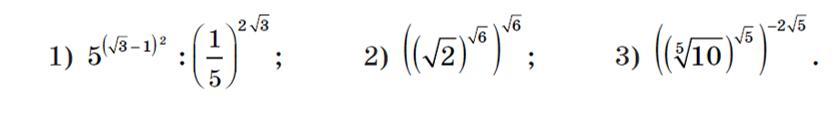
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Қазақ тiлi,
автор: boystoys151212
Предмет: Математика,
автор: asinaruzybaeva
Предмет: Химия,
автор: zajkasuleva
Предмет: Химия,
автор: diana617853
Предмет: ОБЖ,
автор: artmrubtsov