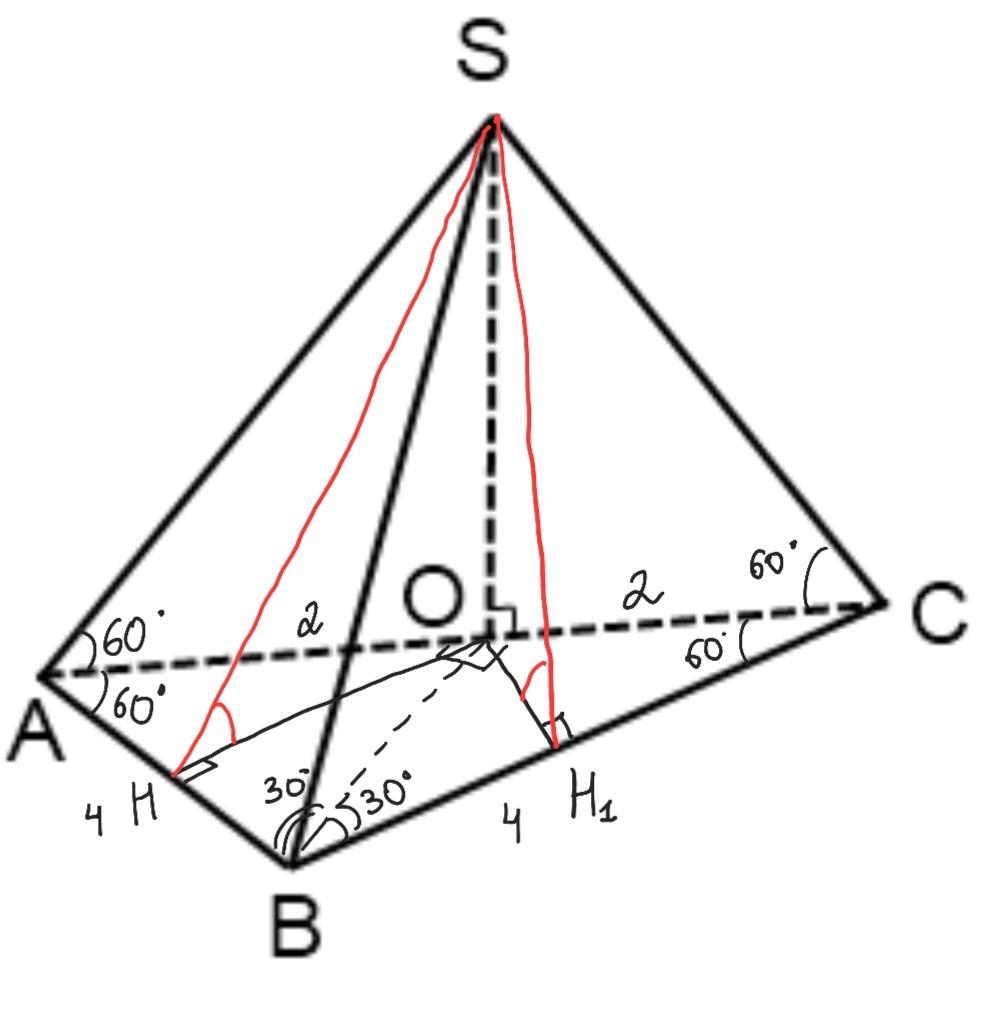
Основа піраміди - рівносторонній трикутник, довжина сторони — 4 см. Одна бічна грань, яка також є рівностороннім трикутником, перпендикулярна основі. Дві інші бічні грані утворюють з основою рівні кути. Визнач площу поверхні піраміди.
Ответы
Дано: треугольная пирамида ABCS, ΔАВС - основание, ΔАВС - равностонний, АВ=4см, ASC - боковая грань пирамиды, ASC⟂АВС, ∠SHO= ∠SH1O.
Найти: Sповерх. ABCS.
Решение.
1) В ΔАВС, поскольку он равносторонний, ВО — это биссектриса, медиана и высота одновременно. Поэтому, АО=ОС= 4:2= 2 см.
В ΔАВО (∠ВОА=90°, т.к. ВО - высота) по т. Пифагора:
ОВ²= АВ²–АО²;
ОВ²= 4²–2²
ОВ²= 16–4;
ОВ²= 12;
ОВ= 2√3 (см).
2) В ΔВОН1 (∠ВН1О=90°):
sin30°= OH1/BO;
0,5= OH1/2√3;
OH1= √3 (см).
2) В ΔSOC, tg60°= SO/OC;
√3= SO/2;
SO= 2√3 (см).
3) В ΔSOH1 (∠SOH1=90°, поскольку ASC⟂АВС) по т.Пифагора:
(SH1)²= SO²+ (OH1)²;
(SH1)²= (2√3)²+(√3)²;
(SH1)²= 12+3;
(SH1)²= 15;
SH1= √15 (см).
4) Sповерх. пирамиды = Sбок.+Sосн.
Sбок.пирамиды= 0,5•Pосн.•d, d — апофема.
Sбок.ABCS= 0,5•(AB+BC+AC)•SH1=0,5•12•√15= 6√15 (см).
Sосн.ABCS= 0,5•OB•AC= 0,5•2√3•4= 4√3.
Sповерх.ABCS= Sбок.ABCS+Sосн.ABCS= 6√15+4√3= 2√3(√5+2). (см) Это приблизительно 30 см (округлено до целых)
Ответ: 2√3(√5+2) см или 30 см.
Рисунок приложено.