решите подробно пожалуйста
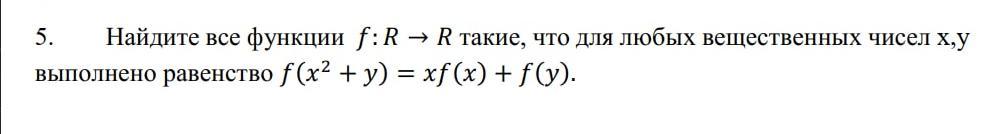
Ответы
Ответ:
Объяснение:
Положим :
Далее :
В соответствии с этим (1) принимает вид
Произведя в последнем равенстве замену и приравняв правые части, получим
Отсюда, либо решением является , либо
С учетом (3) исходное уравнение принимает вид
А с учетом (4) и замены получим
Соответственно, с учетом (5) и (6), уравнение равносильно функциональному уравнению Коши , которое в непрерывных функциях имеет единственное семейство решений
---------------------------------------------------------------------
После получения (2) можно было рассуждать иначе, выполнив преобразования условия:
Устремляя x к нулю, получим с обеих сторон не что иное, как производные:
А это значит, что , откуда, в свою очередь,
Остается подставить в условие задачи:
А по поводу олимпиад - если говорить про школьный уровень, то в целом встретить функциональное уравнение не на олимпиаде практически невозможно, а если речь про университет (или, соответственно, олимпиады), то уж уравнение Коши должно просто автоматом приходить на ум
Ответ:
Объяснение:
Хочется внести и свою лепту, хотя первое решение исчерпывающе (в классе непрерывных функций; впрочем, непрерывность я тоже буду предполагать).
Прошу прощения, если местами решения будут совпадать.
Взяв y=x, получаем уравнение
подставив x=-1, получаем f(0)=0.
Далее, взяв y=0, получаем
что равносильно при положительных x уравнению
А отсюда получается цепочка
Поскольку при
а а также учитывая непрерывность функции, получаем равенство (пока что при положительных x)
Распространение этого равенства на отрицательные x не вызывает затруднений. Точнее, будем по-прежнему считать, что x>0, и докажем, что f(-x)=-xf(1). В самом деле, подставим в равенство f(x²)=xf(x) вместо x минус x:
что и требовалось доказать.
Итак, доказано, что если непрерывная функция удовлетворяет исходному равенству, то она имеет вид
Докажем, что все такие функции удовлетворяют исходному уравнению: