Предмет: Физика,
автор: annabogacenko9
❣️50 баллов ❣️
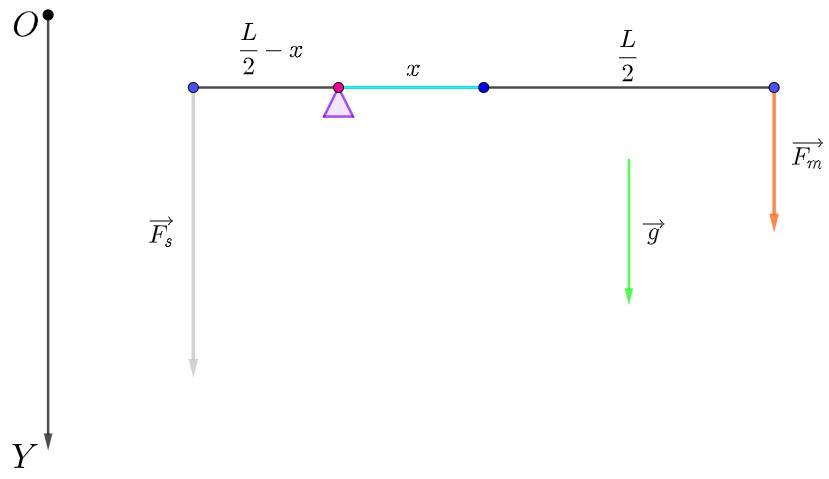
4. До кінців важеля довжиною L=50 см підвішено мідний та срібний куби однакового об'єму. На якi вiдстанi вiд середини важеля треба розмістити точку опори, щоб важіль перебував у рівновазі? Густина міді PM =8900 кг/м3 , а срібла р. =10500 кг/м 3 .
Ответы
Автор ответа:
0
Ответ:
На расстоянии приблизительно 0,02 м от середины рычага нужно разместить точку опоры, чтобы рычаг был в равновесии
Объяснение:
Дано:
0,5 м
8900 кг/м³
10500 кг/м³
Найти:
------------------------------------
Решение:
Масса через плотность:
Масса серебряного кубика:
Масса медного кубика:
На кубики действует сила тяжести (по модулю):
По законам статики:
- моменты равны
- расстояние от середины рычага
Расчеты:
(0,5 м(10500 кг/м³ - 8900 кг/м³)) / (2(10500 кг/м³ + 8900 кг/м³))
0,02 м
Ответ: 0,02 м.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: katababichm
Предмет: Информатика,
автор: cepikmak32
Предмет: История,
автор: av7841292
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: 55day