Предмет: Математика,
автор: mckatekun
знайти похідну неявної функції
Приложения:
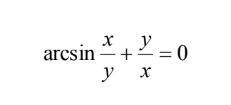
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Найти производную неявной функции:
Здесь у - функция от х ⇒ (у)' = y'.
Понадобятся формулы:
Найдем производную:
Избавимся от знаменателя. Умножим обе части на общий знаменатель:
Получим:
Выражения с y' оставим слева, остальное перенесем вправо:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Литература,
автор: trubnikovakarina3
Предмет: Биология,
автор: kolesnikovnazar06
Предмет: Математика,
автор: Lenochks