Question

D6. Решите задачу векторным методом. Выполните рисунок.
Дан треугольник ABC. Известно, что AB = 6см, BC= 3√3см, Z ABC= 30º.
Найдите длину медианы ВM.

Answer 1

Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Находим длину АС:

AC = √(6² + (3√3)² - 2*6*3√3*cos 30°) = √(36 + 27 - 36√3*√3/2) = √(63 – 54) = √9 = 3.

Далее видим, что треугольник АВС прямоугольный с прямым углом С, так как сумма квадратов АС и ВС равна квадрату АВ.

Отсюда длину медианы ВМ находим по Пифагору.

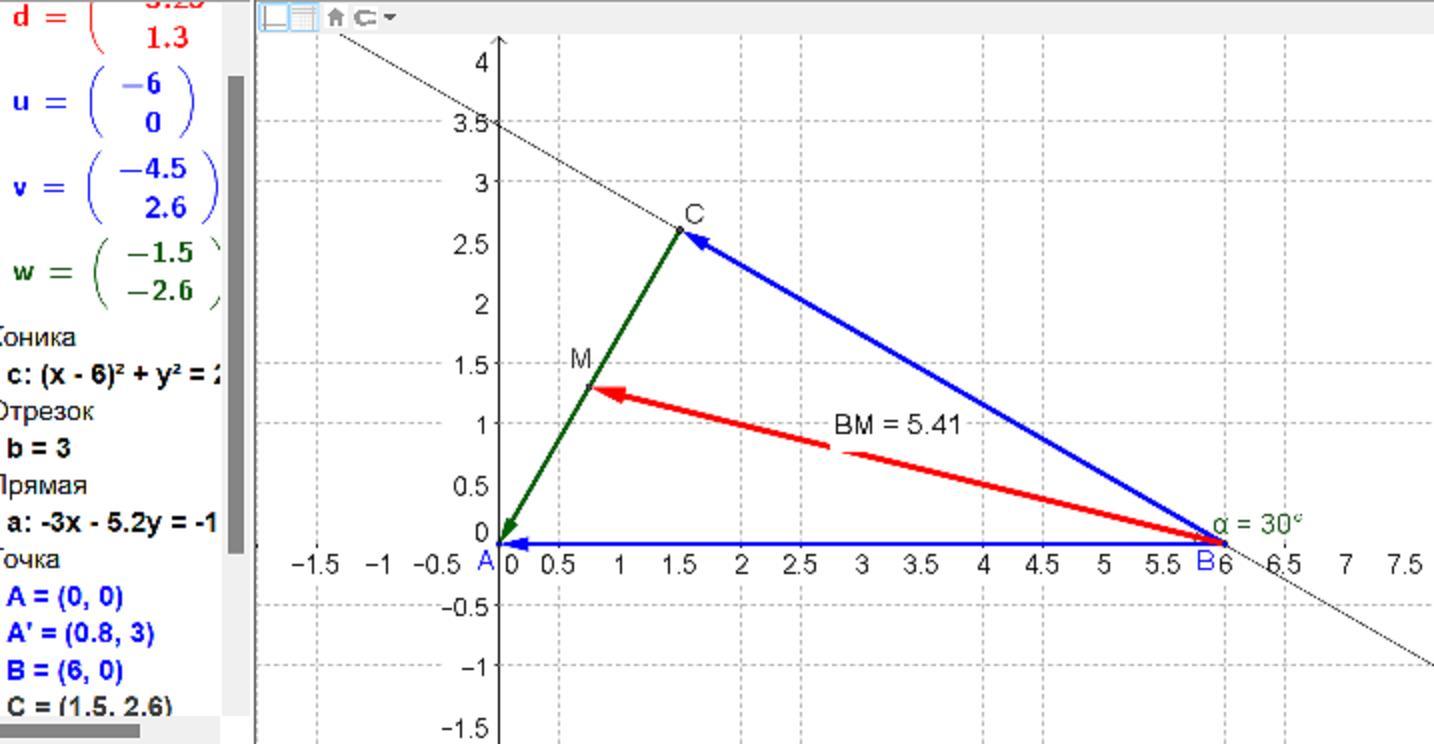
ВМ = √((3√3)² + (3/2)²) = √(27 + (9/4)) = √(117/4) = √117/2 ≈ 5,4083.