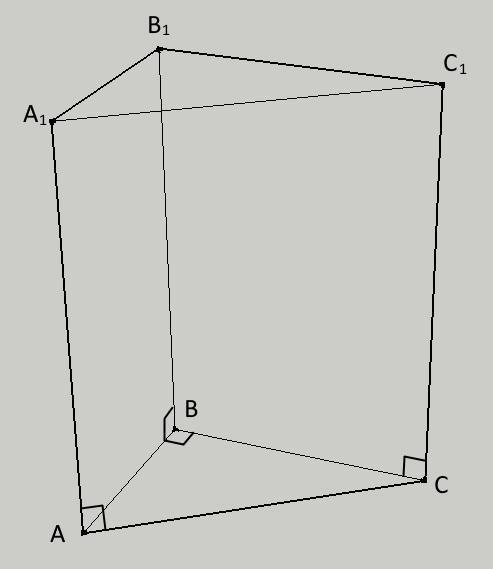
1. Основа прямої призми прямокутний трикутник з катетом 6 см і гіпотенузою 10 см, висота призми 12 см. Знайдіть площу повної поверхні призми.
Допоможіть будь ласка
Ответы
Ответ:
Площадь полной поверхности призмы равна 336 см².
Объяснение:
Основание прямой призмы - прямоугольный треугольник с катетом 6 см и гипотенузой 10 см, высота призмы 12 см. Найдите площадь полной поверхности призмы.
Дано:
AB = 6 см
AC = 10 см
AA₁ = 12 см
-------
Площадь полной поверхности призмы состоит из двух площадей основания S(ABC) и площадей боковых граней S(ABB₁A₁), S(ACC₁A₁), S(BCC₁B₁)
По теореме Пифагора найдем второй катет основания:
BC = √(AC²-AB²) = √(100-36) = 8 см
Площадь основания равна:
S(ABC) = AB·BC/2 = 6·8/2 = 24 см²
Боковые грани являются прямоугольниками, так как призма прямая, найдем их площади:
S(ABB₁A₁) = AB·AA₁ = 6·12 = 72 см²
S(ACC₁A₁) = AC·AA₁ = 10·12 = 120 см²
S(BCC₁B₁) = BC·AA₁ = 8·12 = 96 см²
Площадь полной поверхности призмы равна:
S = 2·S(ABC)+S(ABB₁A₁)+S(ACC₁A₁)+S(BCC₁B₁) = 2·24+72+120+96 = 336 см²