Предмет: Математика,
автор: testtexnosaleprivokz
допоможіть будь ласка рішити завдання з математики срочно будь ласка!!!!
1 завдання розв'язати рівняння
2 завдання знайти похідну функцію
Приложения:
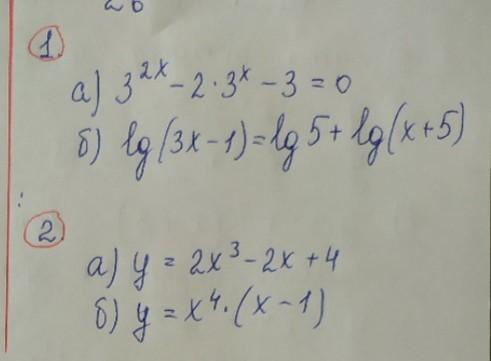
Ответы
Автор ответа:
0
Ответ:
1. Корни уравнений:
а)
б)
2. Производные функций:
а)
б)
Примечание:
По таблице производных:
, где
По правилам дифференцирования:
, где
Пошаговое объяснение:
1.
а)
Замена:
--------------------------
б)
ОДЗ:
, но согласно ОДЗ
и так как:
2.
а)
б)
Похожие вопросы
Предмет: Информатика,
автор: alinabdullaeva100320
Предмет: Другие предметы,
автор: alya7514
Предмет: Математика,
автор: bajbusinovagulsezim
Предмет: Математика,
автор: hdks777
Предмет: Немецкий язык,
автор: litvakzena00