Предмет: Алгебра,
автор: balabay1977
Помогите пожалуйста
Приложения:
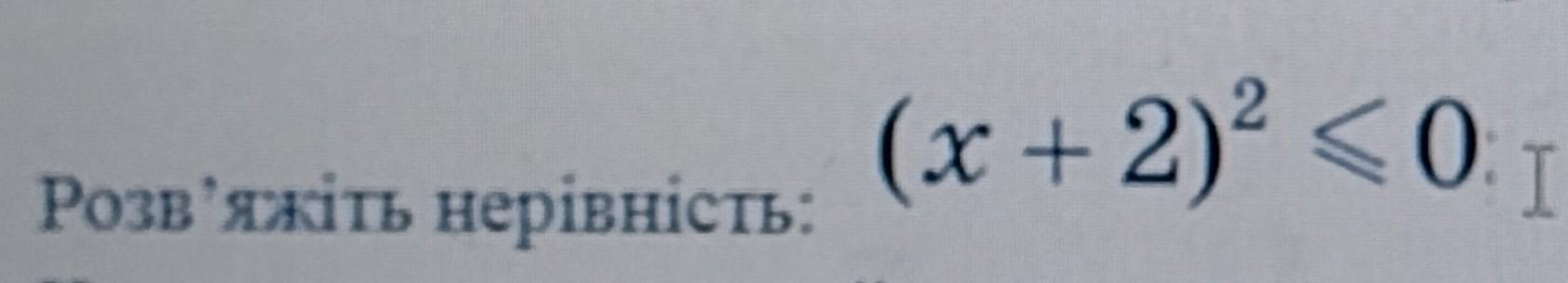
Ответы
Автор ответа:
2
Ответ:
(x+2)²≤0
решите относительно x путем проверки значений на интервалах
x=-2
Автор ответа:
1
Ответ:
Левая часть всегда положительная или равна 0, утверждение верно только когда (x+2)²=0
Проверка значений на интервалах:
Похожие вопросы
Предмет: История,
автор: faneko635
Предмет: История,
автор: Shosya
Предмет: Математика,
автор: nartovaket
Предмет: Английский язык,
автор: qlzmk23315
Предмет: Математика,
автор: Drobot2107