Предмет: Геометрия,
автор: VladZinkov2000
20 балів
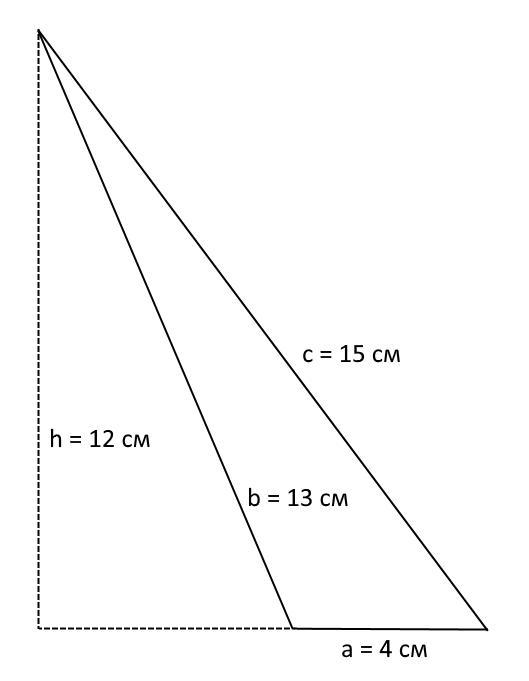
Знайдіть найбільшу висоту трикутника, сторони якого дорiвнюють 4 см, 13 см,
15 см.
Ответы
Автор ответа:
1
Ответ:
Наибольшая высота треугольника равна 12 см.
Объяснение:
Дано:
a = 4 см
b = 13 см
c = 15 см
- ?
-------
Найдем площадь треугольника по формуле Герона:
Где p - полупериметр:
см
см²
Известно, что площадь равна половине произведения стороны на высоту, проведенную к этой высоте:
Из равенства видно, что максимальное значение высоты будет при минимальной стороне, поэтому - это высота, проведенная к стороне a = 4 см:
см
Приложения:
Похожие вопросы
Предмет: Физика,
автор: Ludo4ka09
Предмет: География,
автор: nikolettkos
Предмет: Математика,
автор: vladislavalembetov55
Предмет: Алгебра,
автор: kuryloma