Предмет: Математика,
автор: Igor803
Тема: Однорідні диференціальні рівняння першого порядку.
Завдання: Знайти загальний розв’язок рівняння:
Приложения:
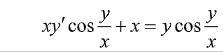
Ответы
Автор ответа:
1
Ответ:
Общее решение дифференциального уравнения:
Пошаговое объяснение:
Замена:
, где
функция от аргумента
.
-----------------------------------------------
- общий интеграл
Похожие вопросы
Предмет: Українська мова,
автор: annapetrushkova
Предмет: Окружающий мир,
автор: povelitek
Предмет: Математика,
автор: dda2002mail
Предмет: Немецкий язык,
автор: Hellstafes
Предмет: Алгебра,
автор: algebra1114