Question

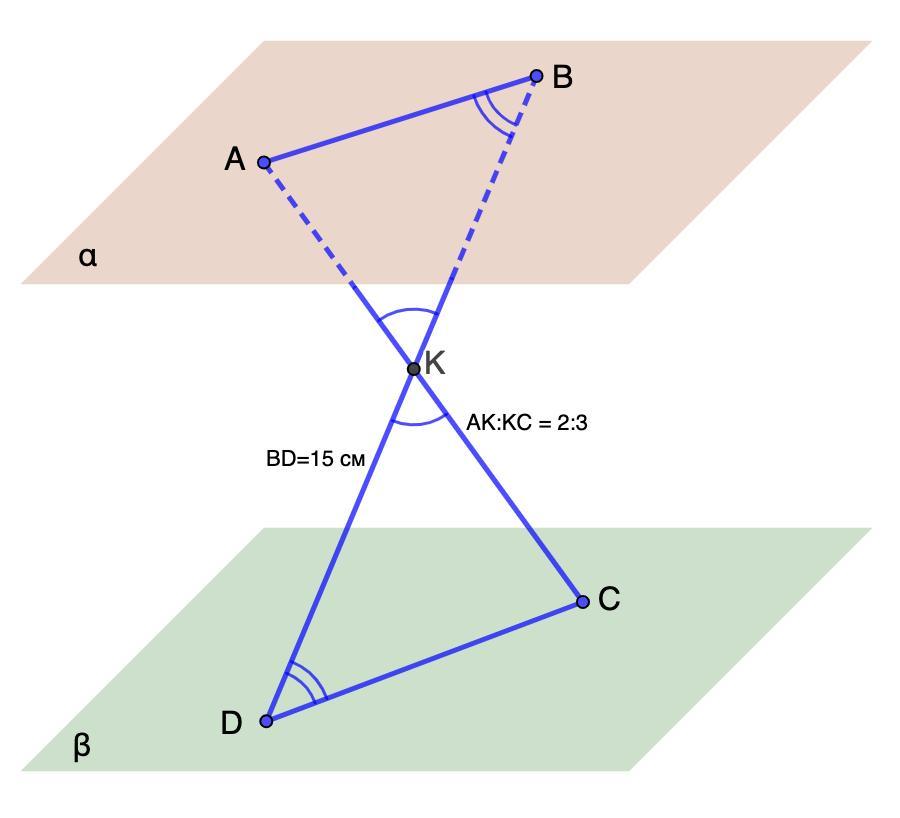
6. На параллельных плоскостях а и в отмечены точки А, В, С и D. Точки А и В лежат на плоскости а, точки С и D лежат на плоскости В. Прямые АС и ВD пересекаются в точке К, лежащей между плоскостями а и В. АК : КС = 2 : 3, BD 15см.
а) Выполните чертёж по условию задачи.

b) Докажите подобие треугольников ДАКВ и ∆СКD.

с) Найдите длину отрезка ВК.​

Answer 1

Ответ:

Доказано ΔАКВ ~ ∆СКD.

Длина отрезка ВК равна 6 см.

Объяснение:

На параллельных плоскостях α и β отмечены точки А, В, С и D. Точки А и В лежат на плоскости α, точки С и D лежат на плоскости β. Прямые АС и ВD пересекаются в точке К, лежащей между плоскостями α и β. АК : КС = 2 : 3, BD 15 см.

а) Выполните чертёж по условию задачи.

b) Докажите подобие треугольников ΔАКВ и ∆СКD.

с) Найдите длину отрезка ВК.​

Дано: α || β;

A, B ⊂ α; C, D ⊂ β;

AC ∩ BD = K;

АК : КС = 2 : 3, BD 15 см.

Доказать: ΔАКВ ~ ∆СКD;

Найти: ВК.

Доказательство:

AC ∩ BD = K

• Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

⇒ AC и BD лежат в одной плоскости.

• Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

⇒ AB || DC

Рассмотрим ΔAKB и ΔCKD.

• Вертикальные углы равны.

⇒ ∠АКВ = ∠DKC (вертикальные).

• Если две параллельные прямые пересечены третьей, то накрест лежащие углы равны.

⇒ ∠АВК = ∠KDC (накрест лежащие при AB || DC и секущей DB)

ΔAKB ~ ΔCKD (по двум углам)

Решение:

ΔAKB ~ ΔCKD.

Запишем отношения сходственных сторон:

$\displaystyle \frac{AK}{KC}=\frac{BK}{KD} =\frac{2}{3}$

Пусть ВК = 2х см, тогда KD = 3x см.

BD = 15 см

2х + 3х = 15

х = 3

⇒ ВК = 6 см, KD = 9 см.

Длина отрезка ВК равна 6 см.

#SPJ1