Помогите пожалуйста.
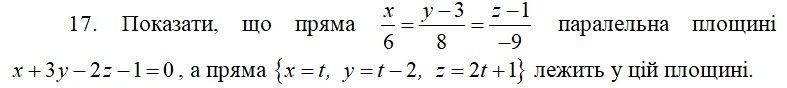
Ответы
Ответ:
1) Если прямая параллельна плоскости, то направляющий вектор прямой ортогонален нормальному вектору плоскости
, значит скалярное произведение вектора нормали и направляющего вектора будет равно 0 . И любая точка данной прямой не удовлетворяет уравнению плоскости . То есть выполняются условия:
Прямая , плоскость
.
Векторы: . Точка на прямой
.
Скалярное произведение векторов равно
Первое условие не выполняется . Значит нет смысла проверять второе условие .
P.S. Чтобы первое условие выполнилось, надо было в условии ординату какого-либо вектора записать со знаком минус .
Прямая не параллельна плоскости
, она её пересекает .
2) Если прямая лежит в плоскости, то направляющий вектор прямой ортогонален нормальному вектору плоскости
, и любая точка данной прямой удовлетворяет уравнению плоскости . Выполняются условия:
Плоскость , прямая
Векторы: , точка на прямой
.
Скалярное произведение векторов равно
Первое условие не выполняется . Значит нет смысла проверять второе условие .
Прямая не лежит в плоскости
, она её пересекает .