Question

Знайти частинний розв'язок диференціального рівняння за початкових умов.
у'' + 4 у' = 4х
Початкові умови
x0 = 0
y0 = 0
y'0 = 1

Answer 1

Ответ:

Частное решение дифференциального уравнения:

$\boldsymbol{\boxed{y = \dfrac{x^{2} }{2} - \dfrac{x}{4} - \dfrac{5e^{-4x}}{16}+ \dfrac{5}{16}}}$

Примечание:

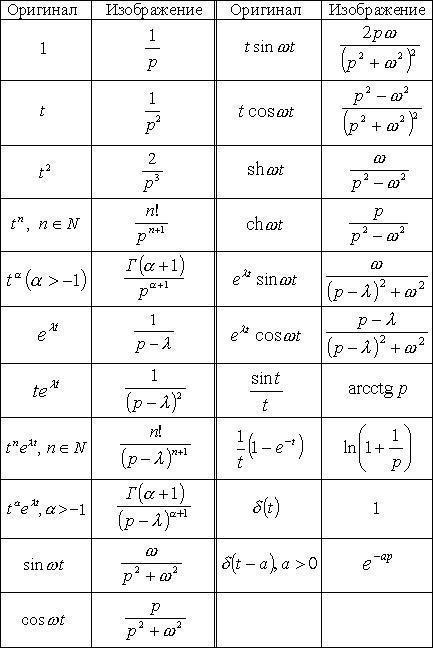
$L \ -$ преобразование Лапласа

Функция $y$ зависит от $x$.

Прямое преобразование Лапласа (связь между оригиналами и изображениями):

$x \xrightarrow{ \ L \ } \dfrac{1}{p^{2}}$

По свойствам преобразования Лапласа:

Если $f(x) \xrightarrow{ \ L \ } F(p)$, то  $\alpha f(x) \xrightarrow{ \ L \ } \alpha F(p)$

Пошаговое объяснение:

$y'' + 4y' = 4x; y(0) = 0; y'(0) = 1$

Для нахождения частного решения данного дифференциального уравнения воспользуемся методом операционного исчисления, а именно преобразованием Лапласа:

$y \xrightarrow{ \ L \ } F(p)$

Дифференцирования оригинала:

$y' \xrightarrow{ \ L \ } pF(p) - y(0) = pF(p) - 0 = pF(p)$

$y'' \xrightarrow{ \ L \ } p^{2}F(p) - p\cdot y(0) - y'(0) = p^{2}F(p) - p \cdot 0 - 1 = p^{2}F(p) - 1$

-----------------------------------------

$p^{2}F(p) - 1 + 4pF(p) = \dfrac{4}{p^{2}}$

$p^{2}F(p) + 4pF(p) - 1 = \dfrac{4}{p^{2}}$

$(p^{2} + 4p)F(p) = \dfrac{4}{p^{2}} + 1 \Longrightarrow F(p) = \dfrac{\dfrac{4}{p^{2}} + 1}{p^{2} + 4p} = \dfrac{\dfrac{p^{2} + 4}{p^{2}} }{\dfrac{p(p + 4)}{1} } = \dfrac{p^{2} + 4}{p^{3}(p + 4)}$

Раскладываем дробь на простейшие:

$\dfrac{p^{2} + 4}{p^{3}(p + 4)} = \dfrac{A}{p^{3}} + \dfrac{B}{p^{2}} + \dfrac{C}{p} + \dfrac{D}{ p + 4} = \dfrac{A(p + 4) + Bp(p + 4) + Cp^{2}(p + 4) + Dp^{3}}{p^{3}(p + 4)}=$

$= \dfrac{Ap + 4A + Bp^{2} + 4Bp + Cp^{3} + 4Cp^{2} + Dp^{3}}{p^{3}(p + 4)}=$

$= \dfrac{Cp^{3} + Dp^{3} + Bp^{2}+ 4Cp^{2} +Ap +4Bp + 4A}{p^{3}(p + 4)}=$

$= \dfrac{p^{3}(C + D) + p^{2}(B+ 4C) +p(A +4B) + 4A}{p^{3}(p + 4)}=$

$\left \{\begin{array}{l} C + D = 0 \\ B + 4C = 1 \\ A + 4B = 0\\ 4A = 4|:4\end{array} \right \ \left \{\begin{array}{l} C + D = 0 \\ B + 4C = 1 \\ 1 + 4B = 0\\ A = 1\end{array} \right \ \left \{\begin{array}{l} D = -C \\ 4C = 1 - B \\ 4B = -1|:4\\ A = 1\end{array} \right \ \left \{\begin{array}{l} D = -C \\ 4C = 1 - B|:4 \\ B = -0,25\\ A = 1\end{array} \right$

$\displaystyle \left \{ {{C = \dfrac{1 - B}{4} = \dfrac{1 + 0,25}{4} = \dfrac{1,25}{4} = 0,3125 } \atop {D = -C = -0,3125}} \right.$

$\dfrac{p^{2} + 4}{p^{3}(p + 4)} = \dfrac{1}{p^{3}} - \dfrac{0,25}{p^{2}} + \dfrac{0,3125 }{p} - \dfrac{0,3125 }{ p + 4} =$

$=\dfrac{1}{p^{3}} - \dfrac{1}{4p^{2}} + \dfrac{5 }{16p} - \dfrac{5 }{16(p + 4)}$

Таким образом $F(p) =\dfrac{1}{p^{3}} - \dfrac{1}{4p^{2}} + \dfrac{5 }{16p} - \dfrac{5 }{16(p + 4)}$

Выполним обратное преобразование Лапласа:

$F(p) \xrightarrow{ \ L^{-1} \ } y$

$\dfrac{1}{p^{3}} \xrightarrow{ \ L^{-1} \ } \dfrac{x^{2} }{2}$

$\dfrac{1}{p^{2}} \xrightarrow{ \ L^{-1} \ } x$

$\dfrac{1}{p} \xrightarrow{ \ L^{-1} \ } 1$

$\dfrac{1}{p + 4} \xrightarrow{ \ L^{-1} \ } e^{-4x}$

Тогда исходная функция равна:

$y = \dfrac{x^{2} }{2} - \dfrac{x}{4} - \dfrac{5e^{-4x}}{16}+ \dfrac{5}{16}$