Предмет: Математика,
автор: kaktussikk
найти производную фунцию
Приложения:
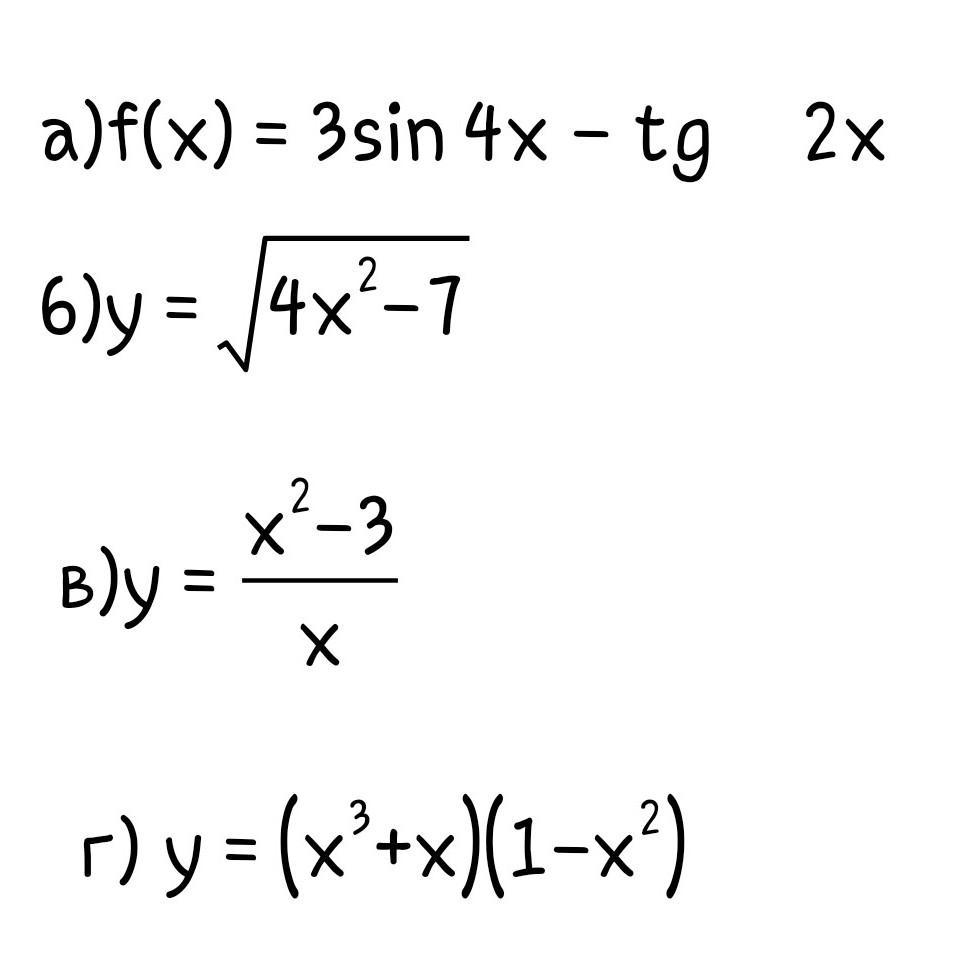
Ответы
Автор ответа:
1
Ответ:
Производные функций:
а)
б)
в)
г)
Примечание:
По таблице производных:
, где
Правила дифференцирования:
, где
функции одной переменной
------------------------------------------------------------------------------------------------
Предполагаем, что в пункте а) имеется в виду следующая функция:
Пошаговое объяснение:
а)
б)
в)
г)
Похожие вопросы
Предмет: Физика,
автор: Voenstal2007
Предмет: История,
автор: a20692026
Предмет: Математика,
автор: tdfyhjvkw2793789
Предмет: Физика,
автор: vikylia1161
Предмет: Биология,
автор: albinahanskaa09