Предмет: Алгебра,
автор: tatiamarch
помогите пожалуйста
Приложения:
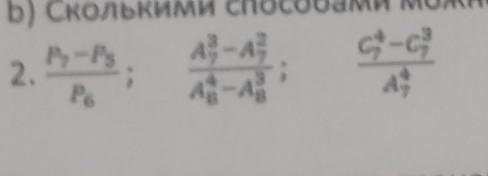
Ответы
Автор ответа:
2
Ответ:
Формулы для вычисления перестановок, размещений и сочетаний:
,
Похожие вопросы
Предмет: Английский язык,
автор: alizanb351
Предмет: Русский язык,
автор: rahimbekovamakpal7
Предмет: География,
автор: darksidee
Предмет: Русский язык,
автор: lilitlilit88
Предмет: Литература,
автор: Kseni0pijhk