Question

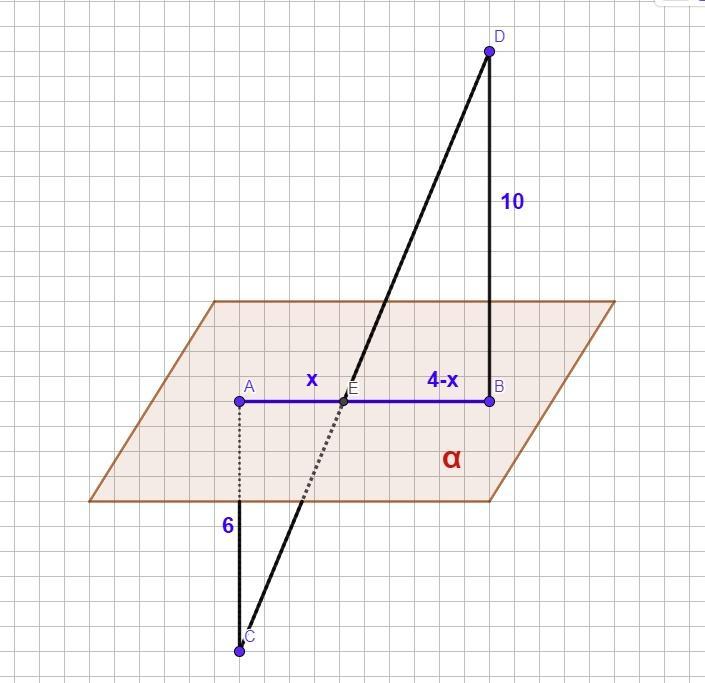
Найди АЕ, если A, B ea, AC||BD, AC=6, BD=10, AB=4, DCa = E​

Answer 1

Ответ:

АЕ= 1,5 (ед)

Объяснение:

Найди АЕ, если A, B ∈ α, AC||BD, AC=6, BD=10, AB=4, DC∩α = E​

• Через две параллельные прямые можно провести плоскость, и притом только одну.

Свойство параллельных прямых:

• Если две прямые параллельны то при пересечении их с третьей (секущей) накрест лежащие углы равны.

• Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Основное свойство пропорции:

• Произведение крайних членов пропорции равно произведению средних членов этой пропорции.

РЕШЕНИЕ

DC пересекает α в точке Е.

Параллельные АС и ВD лежат в одной плоскости, которая пересекает плоскость α по прямой АВ. Т.е. точки А, Е, В лежат на одной прямой.

Рассмотрим ΔАEC и ΔВED.

У них:

• ∠АЕС=∠DEB - как вертикальные

• ∠АCE=∠ВDE - как накрест лежащие углы, образованные при пересечении  параллельных прямых АC и ВD секущей CD.

Следовательно ΔАEC подобен ΔВED по двум углам (первый признак подобия)

Из подобия треугольников следует пропорциональность соответствующих сторон:

$\bf \dfrac{AC}{BD} =\bf \dfrac{AE}{BE}$

Пусть АЕ = х, тогда ВЕ = АВ-АЕ=4-х, тогда:

$\dfrac{6}{10} =\dfrac{x}{4-x}$

Воспользовавшись свойством пропорций, находим х:

10x=6(4-x)

10x=24-6x

16x=24

x=1,5

Таким образом АЕ = 1,5 (ед)