Question

Как написать каноническое уравнение эллипса? Условия задачи в прикрепленной фотографии

Answer 1

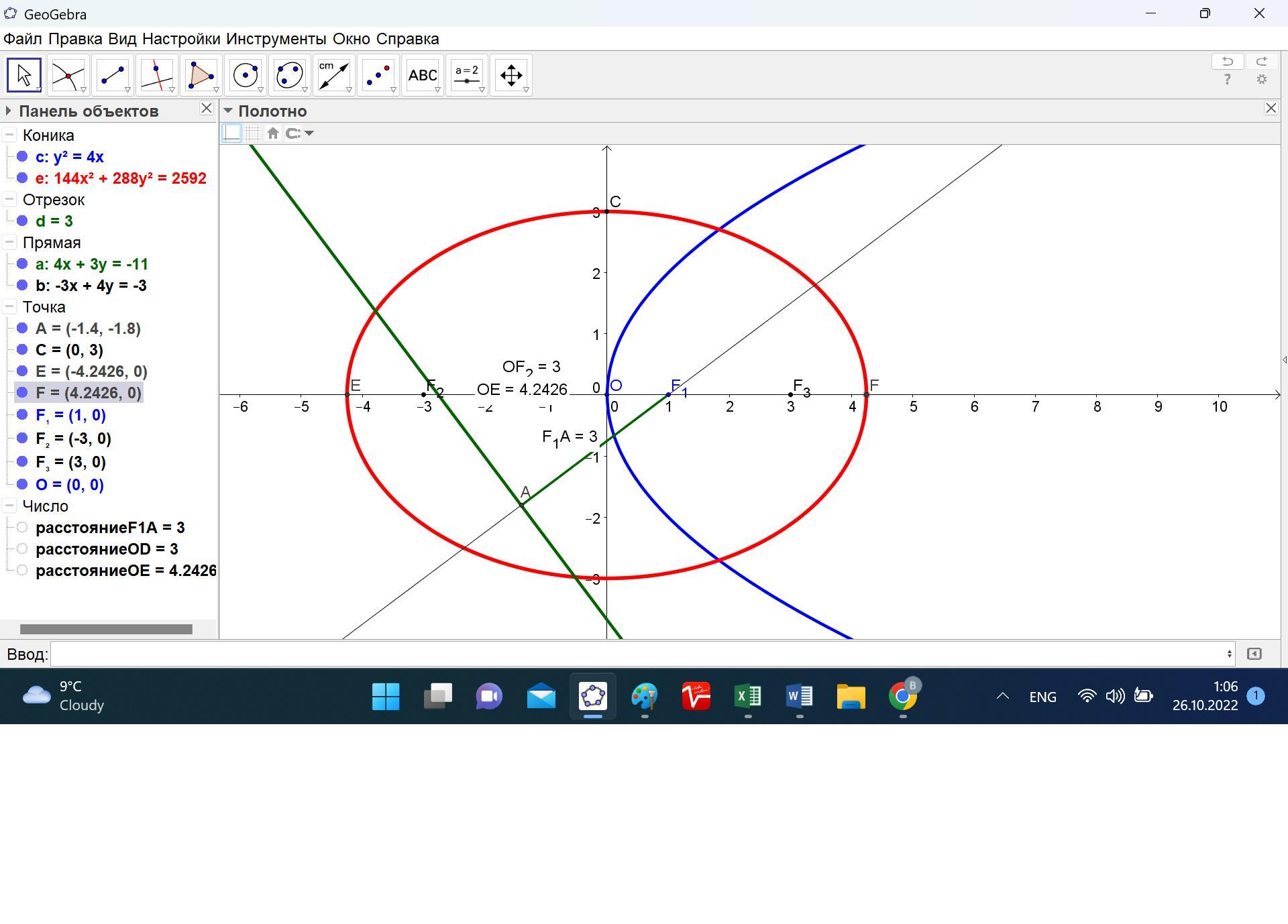
Каноническое уравнение параболы имеет вид  , значит фокус параболы y² = 4x или y² =2*2x имеет координаты   то есть (2/2; 0) или (1; 0).

Найти расстояние от точки M(1; 0) до прямой 4x + 3y + 11 = 0.

Решение.

Расстояние d от точки M1(x1; y1) до прямой Ax+By+C = 0 вычисляется по формуле:

d = 3

c^2 = a^2 – b^2. Значение b найдено и равно 3.

e = c/a, e^2 = c^2/a^2, отсюда a^2*e^2 = a^2 – b^2.

a^2*(e^ - 1) = b^2,  a^2 = b^2/(e^2 - 1).

Подставим данные: a^2 = 3^2/((1/√2)^2) = 9/(1/2) = 18.

Тогда а = √18 = 3√2, с = а*е = 3√2*(1/√2) = 3.

Ответ: уравнение эллипса по заданным условиям имеет вид

(x^2/(√18)^2 + (y^2/3^2) = 1.

Подробнее во вкладке.

cf38d0e97b405dae191108d2a0b49045.docx