Предмет: Математика,
автор: rostikk1986
Похідна неявної функції
Приложения:

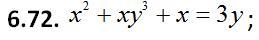
Ответы
Автор ответа:
0
Ответ:
Производные функций:
6.88
6.72
Примечание:
По таблице производных:
, где
По правилам дифференцирования:
, где
Пошаговое объяснение:
6.88
Воспользуемся логарифмическим дифференцированием:
6.72
- пусть функция
Пусть - функция двух переменных
По формуле производной функции заданной неявно:
Похожие вопросы
Предмет: Математика,
автор: zuhrasarsenbaeva72
Предмет: География,
автор: Alifanova1977
Предмет: Математика,
автор: vc95h8rz72
Предмет: Литература,
автор: mavrina990
Предмет: Алгебра,
автор: lolyruff