Предмет: Математика,
автор: unitelnote9128
Поможіть срочно виконати .
Приложения:
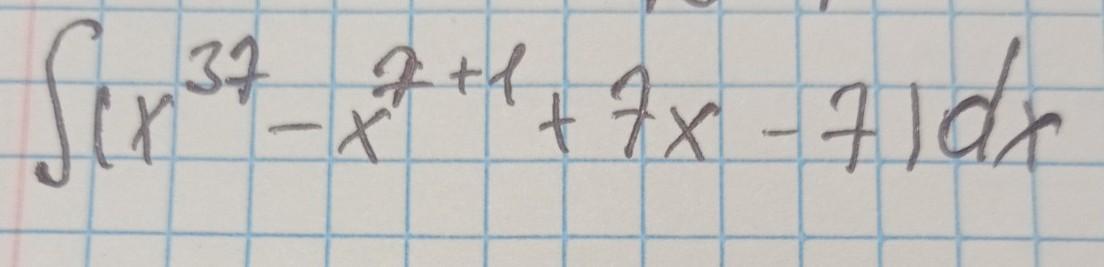
Ответы
Автор ответа:
0
Ответ:
Неопределенный интеграл:
Примечание:
По таблице интегралов:
По свойствам интегралов:
Пошаговое объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: kekskeisodk
Предмет: История,
автор: gromskijvova
Предмет: Математика,
автор: kvshop7005
Предмет: Музыка,
автор: Аноним