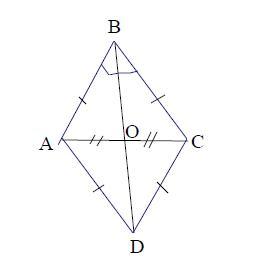
Помогите пожалуйста решить геометрию (дано рисунок решение обязательно)
Один из углов ромба равен 60о, длина его меньшей диагонали равна 10 см. Найти периметр ромба.
Ответы
Ответ:
Объяснение:
Свойства ромба:
1. Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника
2. Диагонали ромба являются биссектрисами его углов
Дано:
ABCD -ромб
∠В = 60°
АС = 10см
Р - ?(см)
----------------
1) Т.к. BD - диагональ ромба и является биссектрисой его углов, то
∠ABD = ∠B/2 = 60°/2 = 30°
2) Т.к. диагонали ромба в тоске пересечения делятся пополам, то
АО =ОС = АС/2 = 10/2 =5(см)
3) Т.к. Диагонали перпендикулярны , то Δ АОВ - прямоугольный.
В прямоугольном Δ-ке против угла в 30° лежит катет, равный половине гипотенузы, следовательно,
АО = АВ/2 → АВ/2 = 5 → АВ = 10(см)
4) Т.к. все стороны ромба равны, то Р = 4*АВ = 4*10 = 40(см)
Ответ: Р = 40см