4. Знайдіть вiдстань від точки перетину діагоналей квадрата до його сторони, якщо
периметр квадрата дорівнює: Bapiaнт 20см Г) 8см Б)5см B)4CM B
Ответы
Ответ:
Вiдстань від точки перетину діагоналей квадрата до його сторони дорівнює 2,5 см
Объяснение:
Знайдіть вiдстань від точки перетину діагоналей квадрата до його сторони, якщо периметр квадрата дорівнює 20см
- Квадратом називається прямокутник, у якого всі сторони рівні.
Властивості квадрата:
- Всі сторони квадрата рівні
- Діагоналі квадрата рівні й точкою перетину діляться навпіл
- Діагоналі квадрата взаємно перпендикулярні
- Діагоналі квадрата є бісектрисами його кутів
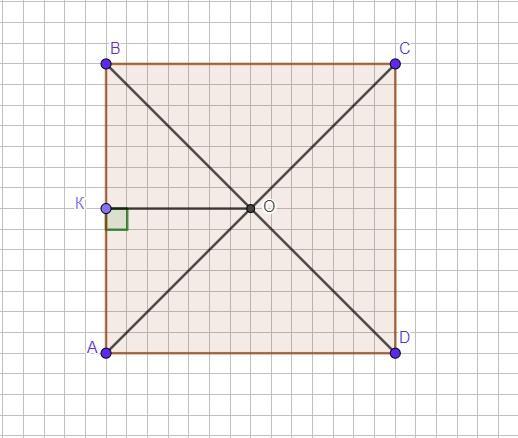
Дано: ABCD - квадрат, О- точка перетину його діагоналей, ОК⊥АВ - відстань від точки О до сторони АВ. Р(АВСD)=20 см
Знайти: ОК
Розв'язок
1.
Так як всі сторони квадрата рівні, то:
Р(АВСD)=4а,
де а - сторона квадрата
АВ=а=Р(АВСD):4=20:4=5(см)
2.
Розглянемо ΔАВО
АО=ВО, АО⊥ВО - за властивістю діагоналей ⇒ ΔАВО - рівнобедрений прямокутний трикутник з основою АВ.
Звідсі висота ОК є одночасно і медіаною (за властивістю), тому: ВК=АК=АВ:2=5:2=2,5 (см)
3.
Розглянемо ΔКВО(∠К=90°)
Так як ВD - бісектриса ∠В, то ∠ОВК=45°
Сума гострих кутів прямокутного трикутника дорівнює 90°, тому:
∠ВОК=90°-∠ОВК=90°-45°=45°
ΔКВО - рівнобедрений з основою ВО.
ОК=ВК= 2,5 (см)
Відповідь: 2,5 см