Question

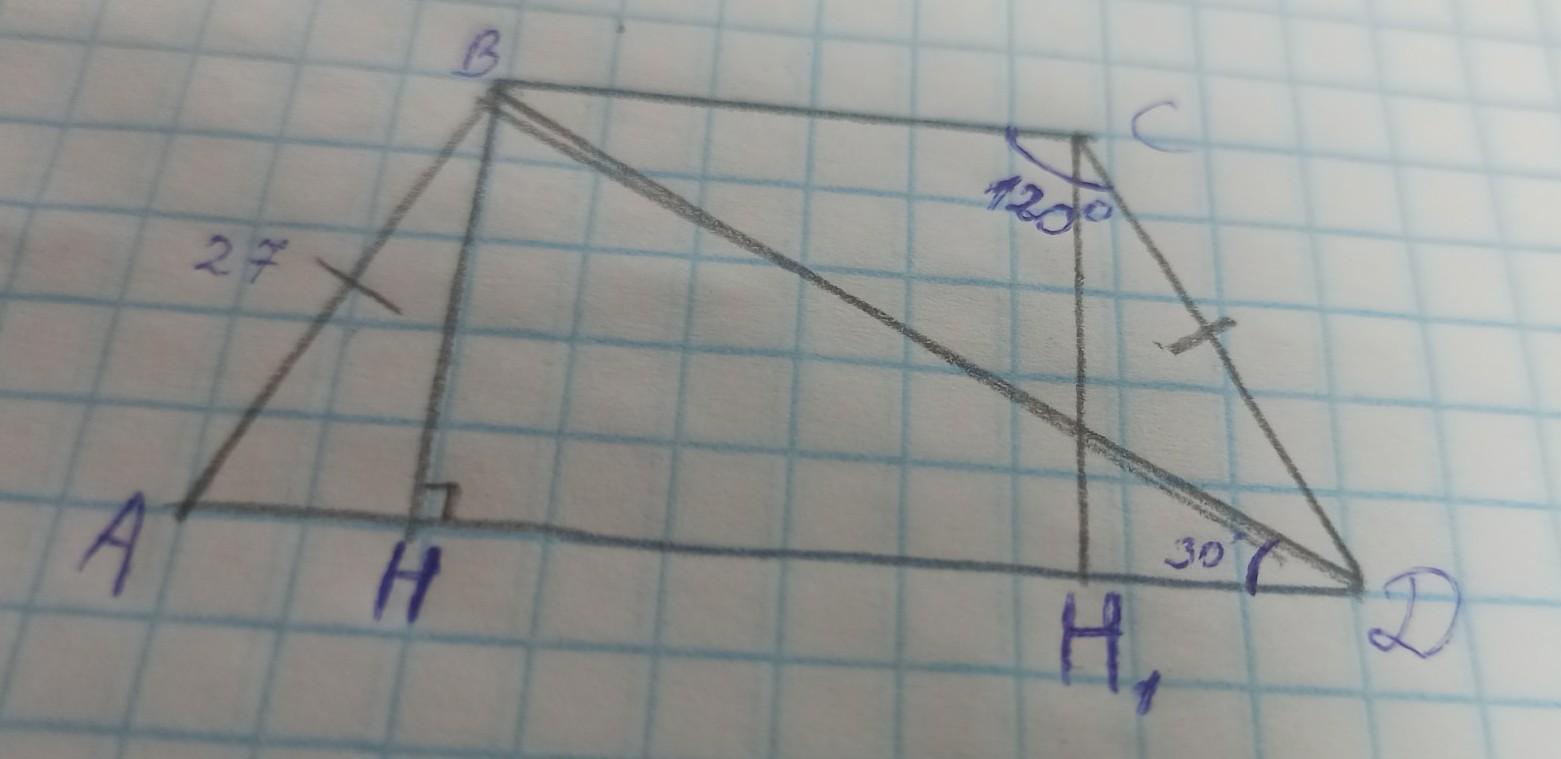
2. В равнобокой трапеции один из углов равен 120 градусов, диагональ трапеции образует с основанием угол 30 градусов. Найдите основания трапеции, если ее боковая сторона равна 27 см.
С черчежом
заранее спасибо​

Answer 1

Ответ:

Сумма углов равнобокой трапеции, прилежащих к одной стороне, равна 180°.

<B=120°

<A=180°-120°=60°

Рассмотрим треугольник ABD.

<BAD=60°

<ADB=30°

Сумма внутренних углов треугольника 180°.

<ABD=180°-60°-30°=90°

По теореме синусов:

$\frac{a}{ \sin( \alpha ) } = \frac{b}{ \sin( \beta ) } = \frac{c}{ \sin( \gamma ) }$

$\frac{27}{ \sin( {30}^{ \circ} ) } = \frac{AD}{ \sin( {90}^{ \circ} ) } \\ \frac{27}{ \frac{1}{2} } = \frac{AD}{1} \\ AD = 2 \times 27 \\ AD = 54$

Проведем высоты AH и CH1.

Так как трапеция равнобокая, AH=DH1 и HH1=BC.

В треугольнике ABH, <BAH=60°, <AHB=90°.

<ABH=180°-90°-60°=30°

$\frac{AH}{ \sin( {30}^{ \circ} ) } = \frac{27}{ \sin( {90}^{ \circ} ) } \\ \frac{AH}{ \frac{1}{2} } = \frac{27}{1} \\ AH = \frac{1}{2} \times 27$

HH1=AD-2AH

$HH_{1} = 54 - 2 \times \frac{1}{2} \times 27 = 54 - 27 = 27$

BC=27

Ответ: AD=54, BC=27