Предмет: Геометрия,
автор: valerykuznets
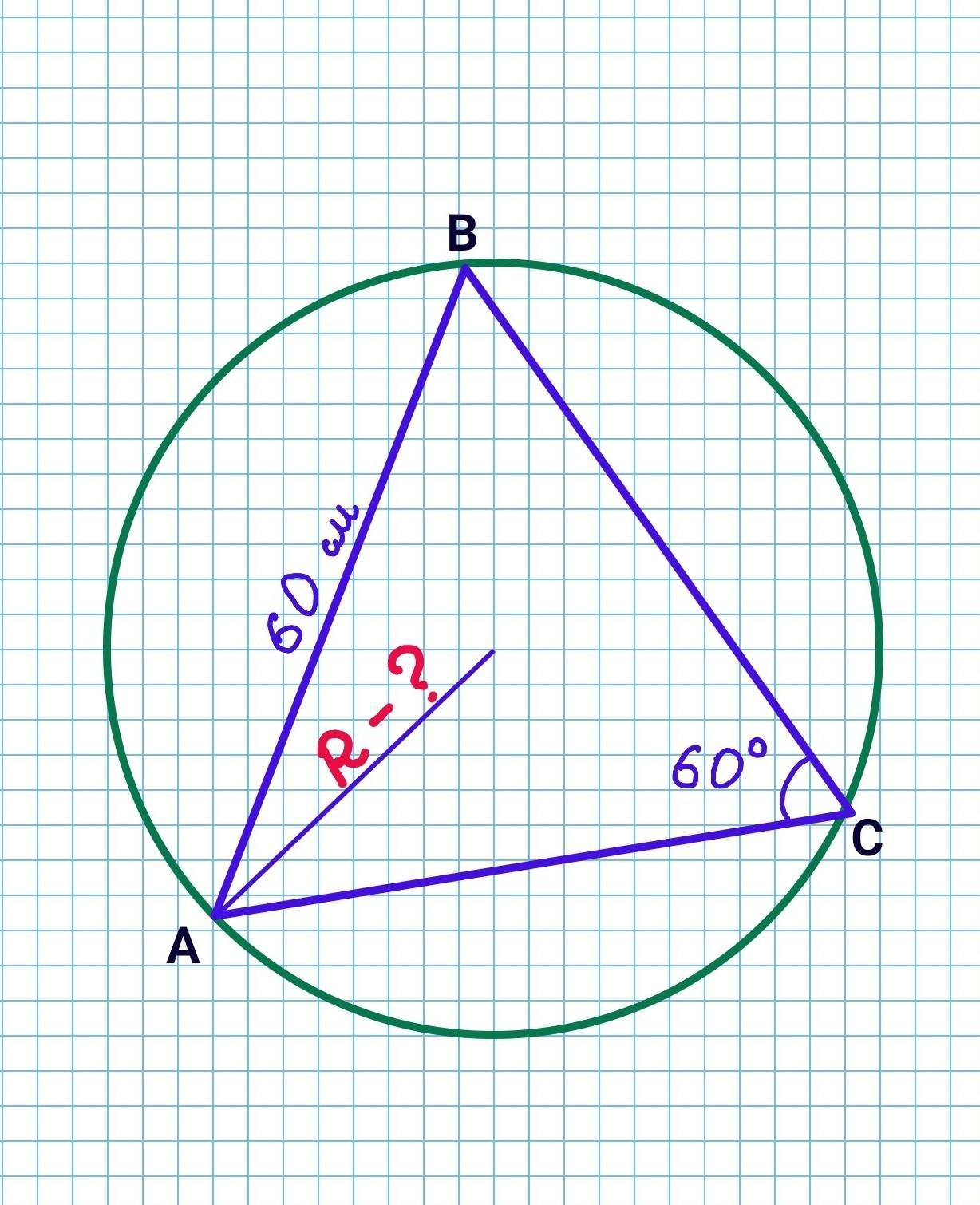
Обчисліть радіус кола описаного навколо трикутника, якщо один із його кутів дорівнює 60°, а протилежна йому сторона 60см
Хєєлпп
Ответы
Автор ответа:
4
Ответ:
Радіус кола описаного навколо трикутника дорівнює 20√3 см
Объяснение:
Обчисліть радіус кола описаного навколо трикутника, якщо один із його кутів дорівнює 60°, а протилежна йому сторона 60 см.
Узагальнена теорема синусів:
У будь-якому трикутнику відношення сторони до синуса протилежного кута дорівнює діаметру кола, описаного навколо цього трикутника:
де R - радіус кола описаного навколо трикутника.
Нехай у трикутнику АВС АВ=60 см, ∠С=60°. Знайдемо радіус кола, описаного навколо трикутника.
За теоремою синусів маємо:
R=20√3 (см)
Приложения:
Мозгокошка:
Здравствуйте!Не могли бы вы помочь с геометрией пожалуйста.Задание в моем профиле.Была бы благодарна за помощь.В любом случае спасибо.Хорошего вам дня
Здравствуйте. вы не могли бы мне помочь Завтра с алгеброй пожалуйста умоляюю
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: История,
автор: ren1viller
Предмет: Математика,
автор: darinaapp
Предмет: Геометрия,
автор: erikabaglan13
Предмет: Английский язык,
автор: bisbiskek2