Логарифмічні рівняння.Будь-ласка с ОДЗ!!
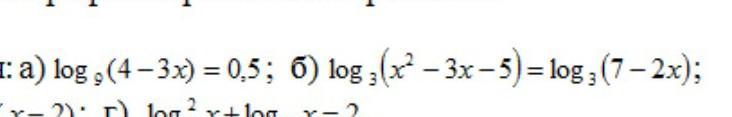
Ответы
Ответ:
Корнем уравнения log₉(4-3x) = 0,5 является число х=1/3.
Корнем уравнения log₃(x²-3x-5) = log₃(7-2x) является число х=(-3).
Пошаговое объяснение:
а) log₉(4-3x) = 0,5
Аргумент логарифма должен быть строго больше нуля.
ОДЗ: 4-3x>0 ⇒ -3x>-4 ⇒ x<1,25
Допишем в правой части уравнения log₉9 (=1) и представим 0,5 в виде степени аргумента этого логарифма (по формуле logₐbˣ=xlogₐb).
log₉(4-3x) = 0,5log₉9
log₉(4-3x) = log₉9⁰'⁵
Справа и слева логарифмы с основанием 9, значит мы можем приравнять их аргументы. Используем свойство х⁰'⁵ = √х.
4-3х = 9⁰'⁵
-3х = √9 - 4
х = -1 : (-3)
х = 1/3 ∈ ОДЗ ✓
Корнем уравнения log₉(4-3x) = 0,5 является число х=1/3.
б) log₃(x²-3x-5) = log₃(7-2x)
Опять же, аргумент логарифма должен быть строго больше нуля. В этом уравнении намного проще сделать проверку вместо ОДЗ, но, так как по условию нужно ОДЗ, мы находим его.
Решим отдельно первое и второе неравенства.
Находим пресечение двух промежутков.
Имеем окончательное ОДЗ:
Возвращаемся к уравнению. Справа и слева логарифмы с основанием 3, поэтому приравниваем их аргументы и решаем квадратное уравнение.
Мы нашли всего один корень, который принадлежит ОДЗ. Поэтому, корнем уравнения log₃(x²-3x-5) = log₃(7-2x) является число х=(-3).