Question

Срочно мне нужно до завтра, иначе я буду не аттестованым, мне нужен полный ответ, желательно на украинском языке??​

Answer 1

Ответ:

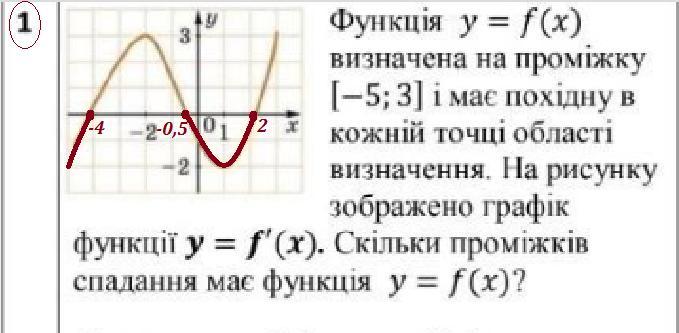
1.  Надо точно понимать, что задан график не функции, а её производной  $\bf y=f'(x)$   .

Функция убывает (спадает) на промежутках, где производная

отрицательна или равна 0 .

Это два промежутка  $\boldsymbol{(-\infty ;-4\ ]}$  и    $\bf [-0,5;\ 2\ ]$  . Смотри рисунок 1 .

Ответ: В) .

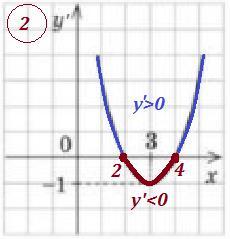
2.  Задан график производной функции   $\bf y=f'(x)$   .

1)  Функция убывает на тех промежутках, где производная

отрицательна или равна 0 , то есть при  $\boldsymbol{x\in [-2\ ;\ 4\ ]}$  , ответ Б) .

2)  Функция возрастает, на тех промежутках, где производная

положительна или равна 0, то есть на каждом из промежутков

 $\boldsymbol{(-\infty ;\ 2\ ]\ ,\ [\ 4\ ;+\infty )}$  , ответ В) .  Смотри рисунок 2 .

3)  Точка максимума  - это точка, при переходе через которую

производная меняет знак с  плюса на минус, то есть  х=2 , ответ Д) .

4)  Точка минимума  - это точка, при переходе через которую

производная меняет знак с минуса на плюс , то есть  х=4 , ответ Г) .

3.  Найти промежутки монотонности функции и точки экстремума .

$y=\dfrac{1}{2}\, x^4-x^3\ \ \ \Rightarrow \ \ \ y'=\dfrac{1}{2}\cdot 4x^3-3x^2=0\ \ ,\\\\2x^3-3x^2=0\ \ ,\ \ x^2\, (2x-3)=0\ \ \Rightarrow \ \ \bf x_1=0\ ,\ x_2=1,5$  

Знаки производной:   $---[\ 0\ ]---[\ 1,5\ ]+++$  

Функция возрастает при  $\boldsymbol{x\in[\ 1,5\, ;+\infty \, )}$  .

Функция убывает при   $\boldsymbol{x\in (-\infty ;\ 1,5\ ]}$  .

Производная функции меняет знак только при переходе через точку  х=1,5 с минуса на плюс , значит точка х=1,5  - точка минимума .

$\boldsymbol{y(min)}=y(1,5)=\dfrac{1}{2}\cdot (1,5)^4-(1,5)^3=\bf -0,84375$   .