Предмет: Алгебра,
автор: efwfwfwe
Дам 40 баллов!!!
Пожалуйста очень прошу нужно упростить и найти значение выражения
Приложения:
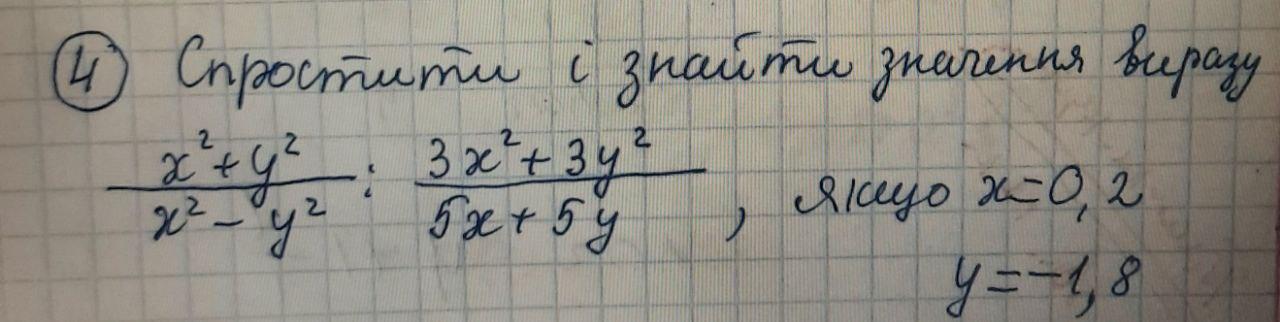
Ответы
Автор ответа:
1
надіюсь зрозумілий почерк
Приложения:
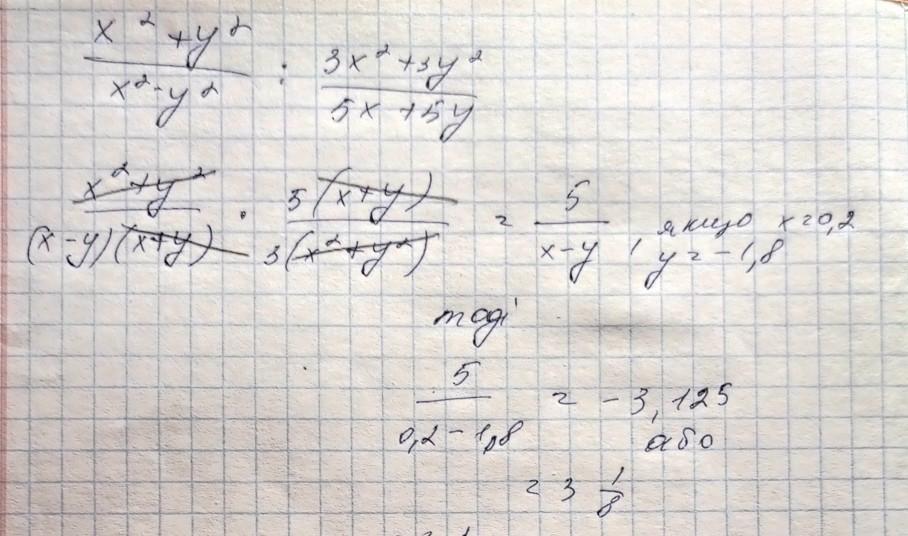
Автор ответа:
1
Щоб поділити дроби, потрібно помножити їх на обернений дріб
За формулою
Розкладемо на множники, а також винесемо що можливо за душки, щоб мати спільні множники
Навхрест скорочуємо що можливо
Підставляємо значення і вираховуємо
Похожие вопросы
Предмет: Английский язык,
автор: nuraiym1469
Предмет: Биология,
автор: ulanaperepelica28
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: amangeldynuraj6
Предмет: Английский язык,
автор: mrdarj8