помогите пожалуйста срочно!!!
Чертить график обязательно
2. Найдите множество точек координатной плоскости, которое задано системой неравенств.
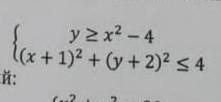
Ответы
Ответ:
Найдите множество точек координатной плоскости, которое задано системой неравенств:
у ≥ х²–4
(х+1)²+(у+2)² ≤ 4
Объяснение:
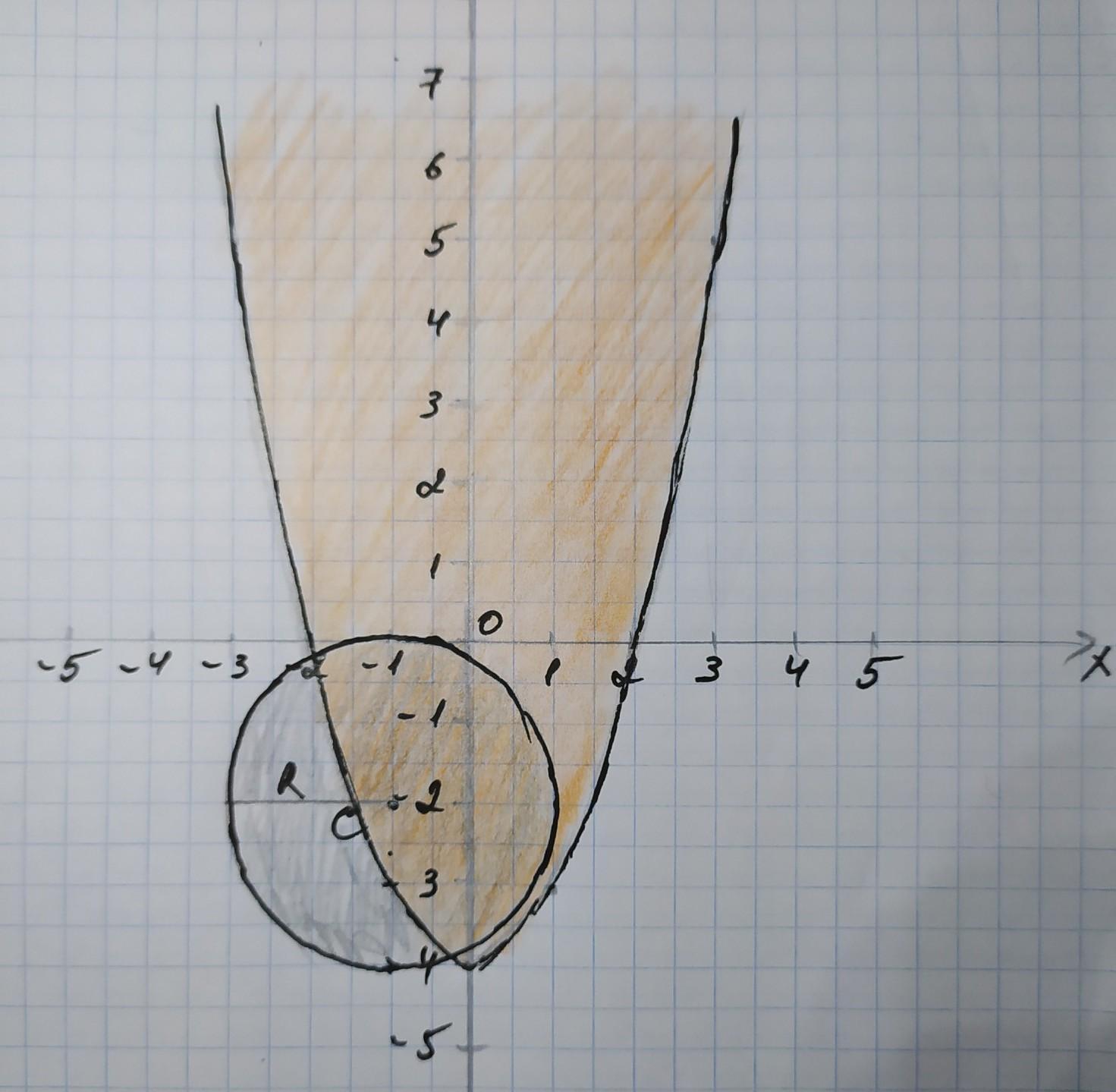
Для построения графиков подберём точки к каждой формуле, заменив их на уравнение: у=х²–4 и (х+1)²+(у+2)² = 4
у=х²–4:
х=0 → у= –4; х=1 → у= –3; х=2 →у=0; х=3 →у=5;
х= –1 →у= –3; х= –2 →у=0; х= –3 →у=5
(х+1)²+(у+2)² = 4 – графиком этой формулы является окружность с центром координат в точке С (–1; –2) и радиусом 2.
Если (х+1)²+(у+2)² ≤ 4, то заштриховываем серым карандашом ту область, которая находится в середине круга. Эта заштрихованная область будет являться множеством точек этого неравенства.
Теперь найдём множество точек в неравенстве
у ≥ х²–4.
Для этого выберем любую координату, например вершины параболы (0; –4). Здесь у= –4, а в неравенстве указано, что он должен быть больше, значит выбираем точку с координатой у = –3 например и заштриховываем всю область над параболой оранжевым карандашом – это и будет являться множеством точек в неравенстве параболы.
Область заштрихованная одновременно и серым, и оранжевым карандашом показывает множество точек решения системы, то есть точек пересечения неравенств.