Предмет: Алгебра,
автор: saman110
Найти производную высшая математика
Приложения:
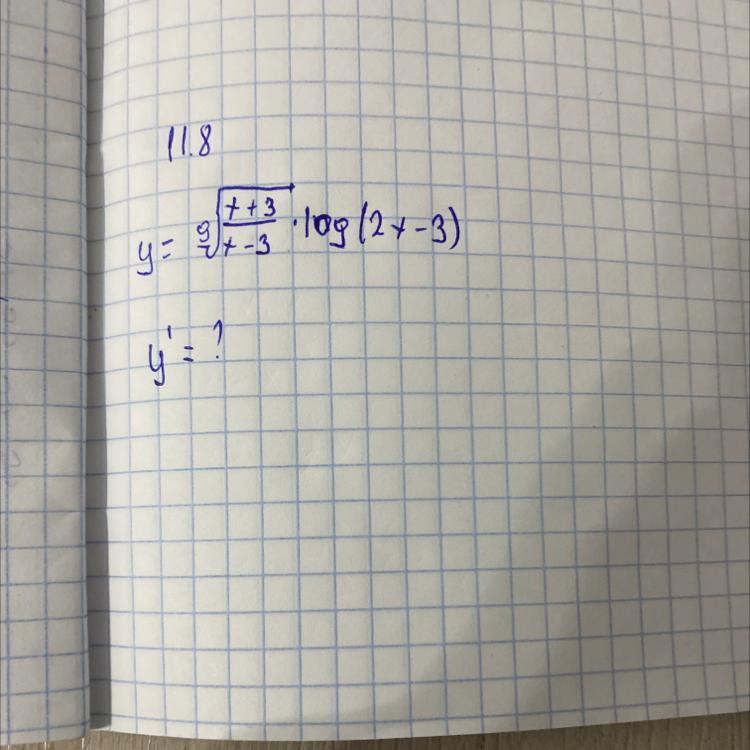
Ответы
Автор ответа:
1
Ответ:
Производная дроби равна ,
,
Похожие вопросы
Предмет: Українська література,
автор: mahadirol965
Предмет: Английский язык,
автор: Savvier1831
Предмет: Русский язык,
автор: alionaponomaren5205
Предмет: ОБЖ,
автор: Vladukx
Предмет: Биология,
автор: nekichav12