Предмет: Геометрия,
автор: sk01040839
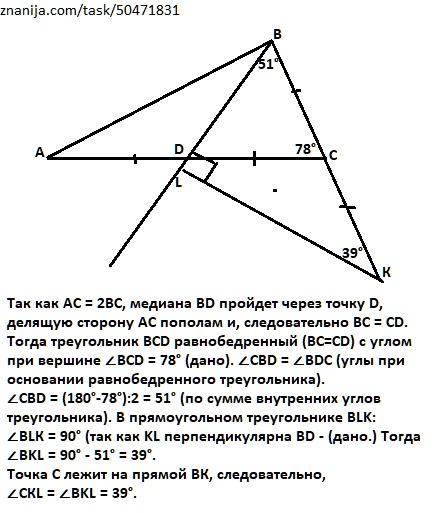
Дан треугольник АВС, где 2 ВС = АС и угол С = 78°. На луче ВС отложили отрезок СК = СВ. После чего из точки К провели перпендикуляр к прямой, содержащей медиану треугольника А ВС, проведённую из вершины В, и на пересечении получили точку L. Чему равен угол CKL? Ответ выразите в градусах.
Ответы
Автор ответа:
0
Ответ:
∠СКL = 39°.
Объяснение:
Так как АС = 2ВС, медиана ВD пройдет через точку D, делящую сторону АС пополам и, следовательно ВС = СD.
Тогда треугольник ВСD равнобедренный (ВС=CD) с углом при вершине ∠BCD = 78° (дано). ∠CВD = ∠BDС (углы при основании равнобедренного треугольника). ∠CBD = (180°-78°):2 = 51° (по сумме внутренних углов треугольника). В прямоугольном треугольнике BLK: ∠BLК = 90° (так как KL перпендикулярна BD - (дано.) Тогда
∠ВKL = 90° - 51° = 39°.
Точка С лежит на прямой ВК, следовательно, ∠СКL = ∠BKL = 39°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kamilalf6161
Предмет: Английский язык,
автор: 9yyicyocyoa
Предмет: Українська література,
автор: nazariishevchuk
Предмет: География,
автор: cyk47
Предмет: Математика,
автор: rfrfrfrfrfrfrfrfrrg