Благаю, допоможіть!
( розв'яжіть нерівність методом інтервалів) ТІЛЬКИ Г)))
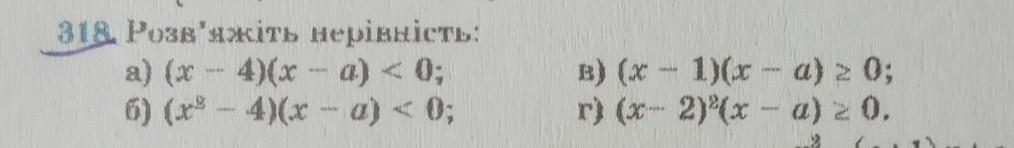
Ответы
Ответ:
Не нарушая общности рассуждений, считаем, что . Если бы было
, то рассуждения были бы такими же , но нужно было бы дать поправку на знак .
Применяем метод интервалов.
Необходимо найти нули функции . Это будут числа
.
Так как конкретного значения числа а мы не знаем, то рассмотрим 3 случая.
1 случай. Число а находится правее числа 2 , то есть .
Тогда считаем знаки на промежутках:
Так как знак неравенства , то выбираем промежуток, где стоит знак плюс и не забываем, что при х=2 функция равна 0 , тогда
.
P.S. Знаки можно определить, если вместо числа а представить себе любое число, большее 2 , например, число 6 .
2 случай. Число а=2 . Тогда имеем
3 cлучай. Число а находится левее числа 2, то есть .
Знаки функции:
Ответ: при имеем
.
при имеем
.