Помогите
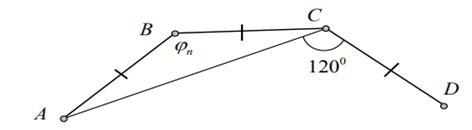
Точки А, В, С, D - сусідні вершини правильного многокутника (саме у такій послідовності). Відомо, що кут ACD=120. Скiльки сторін у цього многокутника?
Точки А, В, С, D – соседние вершины правильного многоугольника (именно в такой последовательности). Понятно, что угол ACD=120. Сколько сторон у этого многоугольника?
Ответы
Ответ:
9
Пошаговое объяснение:
Нехай φn — градусна мiра внутрiшнього кута правильного n-кутника. Тоді, як відомо, має мiсце рівність. φn = (n − 2) · 1800/ n ,
звідки ∠ABC = ∠BCD = φn = (n−2)·1800/ n . Розглянемо трикутник ABC . В ньому: ∠ABC = φn ; AB = BC (як довжини сторін правильного n-кутника). Звідки △ ABC є рівнобедреним. I тому справджуються рівності
∠BAC = ∠BCA = (1800 − φn ) / 2 = 900 – 1/2 φn.
∠BCD = ∠BCA + ∠ACD = 900 – 1/2 φn + 1200 = 2100 – 1/ 2 φn.
З iіншого боку — ∠BCD = φn . Тому справджується рiвнiсть 2100 – 1/2 φn = φn ⇒ 3/2 · φn = 2100 ⇒ φn = 1400 ,
звiдки (n−2)·180/n = 140 ⇒ (n − 2) · 9 = n · 7 ⇒ 2n = 18 ⇒ n = 9.
Отже, правильний многокутник, який задовольняє умову задачі, є 9 - кутником (має 9 сторін).
II спосiб — «за допомогою вписаних кутiв описаного кола