Предмет: Математика,
автор: slobodyanbogdan01
срочно:
Установіть вiдповiднiсть мiж функціями (1-3) та похідними (А-Г) цих функцій.
Приложения:
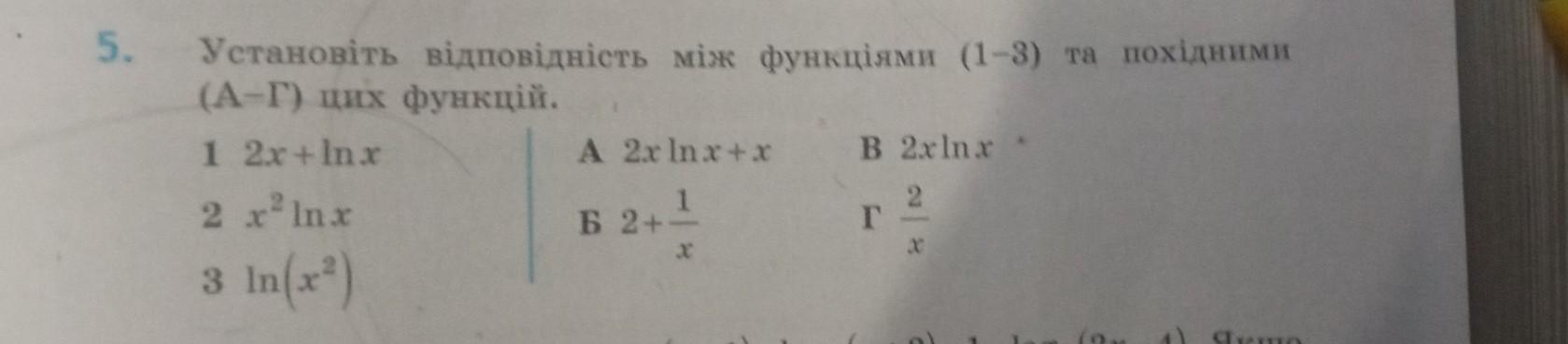
Ответы
Автор ответа:
2
Ответ:
1Б: производная функции y=2x+ln x это y'=2+1/x.
2A: производная функции y=x²ln x это y'=2xln x+x.
3Г: производная функции y=ln(x²) это y'=2/x.
Пошаговое объяснение:
Правила нахождения производных, которые нам понадобятся:
Используя вышеуказанную таблицу, находим производные функций.
1) y=2x+ln x
1Б: производная функции y=2x+ln x это y'=2+1/x.
2) y=x²ln x
2A: производная функции y=x²ln x это y'=2xln x+x.
3) y=ln(x²)
3Г: производная функции y=ln(x²) это y'=2/x.
Похожие вопросы
Предмет: Информатика,
автор: lynawwrxx
Предмет: Химия,
автор: igra11419
Предмет: Алгебра,
автор: lavrivtanya9
Предмет: История,
автор: virctatana450
Предмет: Русский язык,
автор: angelgagik