Предмет: Алгебра, автор: Nellaaaa

УМОЛЯЮ РЕШИТЕ Диагонали AC и BD равнобокой трапеции ABCD пересекаются в точке O. Известно, что AD:BC=5:3. Окружность ω с центром O, проходящая через вершины A и D, пересекает продолжение основания BC за точку B в точке K. Оказалось, что BK=BO. Найдите отношение основания AD к радиусу окружности ω.

antonovm: 7 : 9

Ответы

Автор ответа: antonovm

Ответ:

7 : 9

Объяснение:

Приложения:

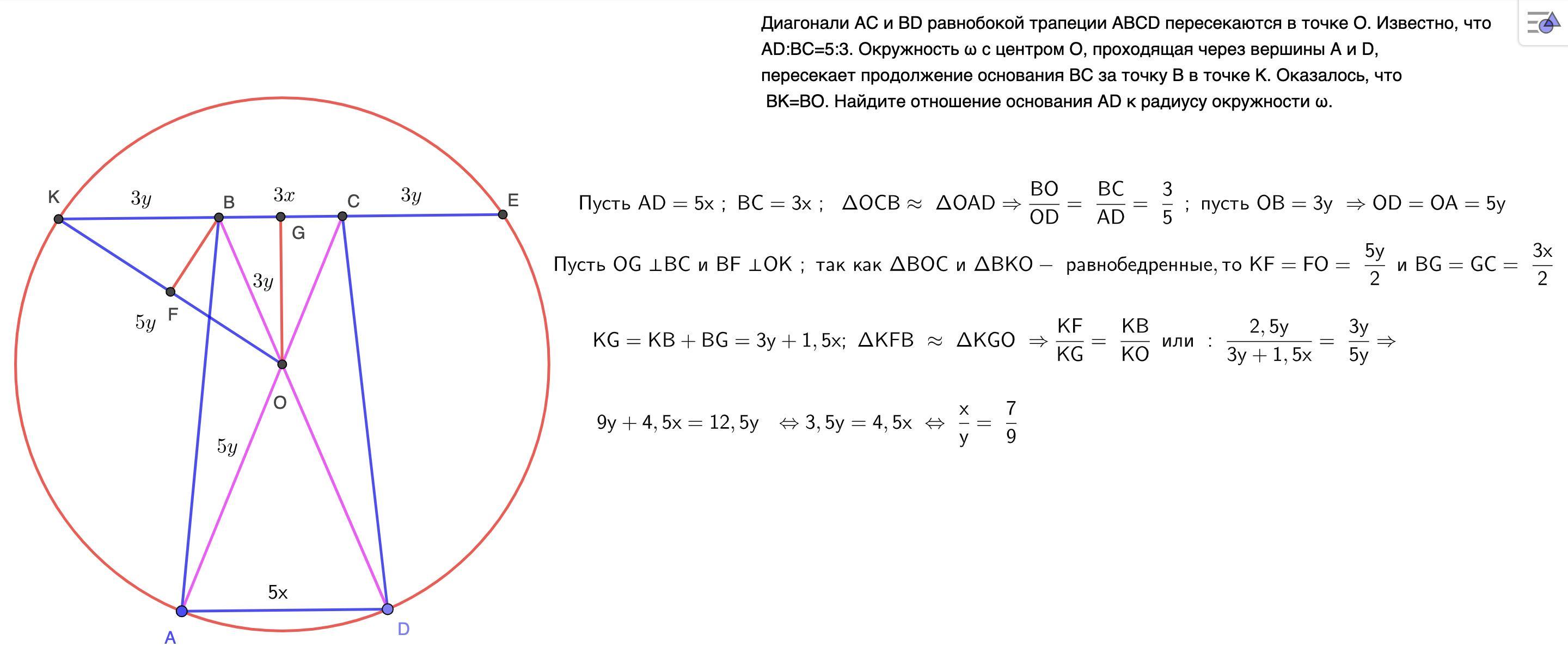
antonovm: Может быть стоит добавить : AD/AO = 5x/5y = x/y = 7/9

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Английский язык, автор: rvitalinar2008

СРОЧНО! даю 20 баллов
B. Paul is writing to a friend.
I'm sorry we weren't here ... May! There aren't so many events ... this month, but there's a fishing boat race .. next Saturday....
Friday we're going riding. (Do you remember? I had some riding lessons ... last summer.) I'd like to be here ... October, when there's a big tennis tournament. They have the tournament ... every October.
C. At a travel agent's.
'Right! your plane leaves ... 14.00. You should check in 1 1/2 hours ... departure time, so you need to be at the airport ... 12.30. You can wait in the departure lounge ... check-in time ... departure
time.
You'll probably wait there ... about 13.50. Now, about getting to the airport. There's an airport bus that leaves the terminal ...
11.00. You could catch that. I know there's always a lot of traffic going to the airport ... the morning, ... about 8.00 ... about 10.00.
However, you'll be going ... that period, so you'll be O.K.'
D. In a coffee bar.
Where have you been? We agreed to meet at 2.30. I've been waiting for you ..
..hours! Well, not exactly hours, but ... 2.35. Let me
see _
. 2.35.
... now: that's forty minutes. I've drunk three cups
of coffee.
.. that time and got very bored. If I'd brought a book I
could at least have been reading ... forty minutes. Anyway, what's your excuse?'
'My excuse? I've been waiting for you ... thirty minutes, in the street. We agreed to meet on the street corner, didn't we? Any-way, ... next week let's meet ... Tuesday. That's easier for me than Wednesday. See you .. next Tuesday, then.'
'What? Are you going already? Aren't you going to stay ... a few minutes?'
'No, I can't! I've got the dentist ... this afternoon. I'll have to wait ... Tuesday for your news!'

2 года назад

Предмет: Математика, автор: happyann06011

-1,8(х - 2,5) = 18,54.
помогите пожалуйста

2 года назад

Предмет: Математика, автор: kenmamiku

МАКСИМАЛЬНО СРОЧНО МНОГО БАЛОВ!!
чому дорівнює сума коренів рівняння х^2+3х -5=0

2 года назад

Предмет: Математика, автор: Аноним

Найди весь путь если 8%пути составляет 48км

8 лет назад

Предмет: Физкультура и спорт, автор: gogohiagiorgi2018

Почему нельзя замедлять бег перед финишной прямой в беге на короткие дистанции? 35б

8 лет назад