С подробным объяснением , как находить а и d? , ещё я не понимаю , когда строить график если из этого получили функцию , асимптоты делаем опираясь на полученную функцию или на условие задания? И как выделить целую часть ?

Ответы
Ответ:
- асимптоты .
Графиком дробно-линейной функции вида является
гипербола . Её удобно строить, когда выделена целая и дробная
части заданной дроби, и она имеет вид .
Асимптоты такой гиперболы - прямые, параллельные осям координат .
Вертикальная асимптота находится из уравнения . В нашем случае это уравнение
. Так как указано, что асимптотой является прямая х=1 , то подставляем вместо х число 1 и найдём d :
.
Горизонтальная асимптота находится из уравнения . В нашем случае это уравнение
. По условию задано уравнение
асимптоты у=3 , тогда .
Получили дробно-линейную функцию .
Преобразуем функцию , выделив целую часть .
Гиперболу можно построить или по точкам, либо с помощью параллельного переноса .
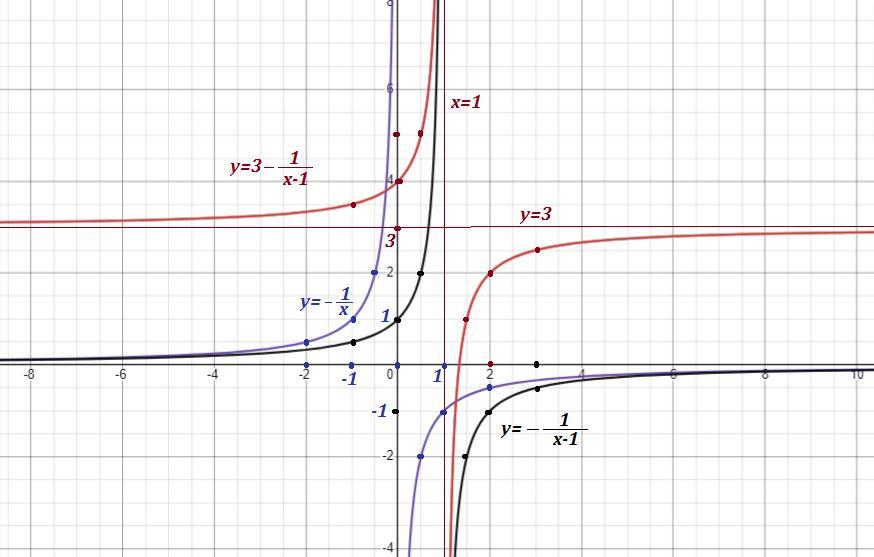
Сначала строим гиперболу , расположенную во 2 и 4 четвертях ( из-за знака минус ) . Проходит через точки (-1 ; 1 ) , (-1/2 , 2) , (-2 ; 1/2 ) , ( 1 ; -1 ) , ( 2 ;-1/2 ) , (1/2 ; -2 ) . Асимптотами будут оси координат : х=0 , у=0 . Cиний график .
Затем сдвигаем гиперболу на 1 единицу вправо вдоль оси ОХ , получим гиперболу . То есть все выше указанные точки сдвигаются на 1 вправо вдоль ОХ . Например, точка (-1 ; 1 ) перейдёт в точку ( 0 ; 1 ) , а точка ( 1 ;-1 ) перейдёт в точку ( 2 ; -1 ) и так далее . Асимптотами будут прямые х=1 и у=0 . Чёрный график .
А теперь, если предыдущую гиперболу сдвинуть вдоль оси ОУ на 3 единицы вверх , то получим заданную гиперболу .
Точка ( 0; 1 ) перейдёт в точку ( 0 ; 4 ) , а точка ( 2 ;-1 ) перейдёт в точку
( 2 ; 2 ) , и так далее .
Обратите внимание на слагаемое 3 (целая часть) и на то , что горизонтальная асимптота имеет уравнение у=3 . Красный график .