это здание нужно решить подробно с рисунком

Ответы
Ответ:
1) высота усечённого конуса равна 12 (ед)
2) угол между образующей и плоскостью основания конуса равен
arccos (1/7)
Объяснение:
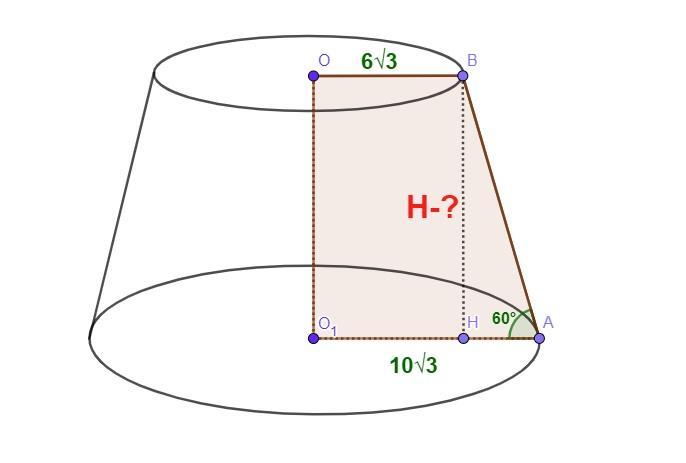
1) Радиусы оснований усечённого конуса 10√3 и 6√3, а образующая наклонена к плоскости основания под углом 60°. Найти высоту усечённого конуса.
Пусть О и О₁ - центры оснований усечённого конуса. ОО₁ = Н - высота усечённого конуса.
В и А - точки, взятые на соответствующих окружностях. Тогда ОВ - радиус верхнего основания усечённого конуса, О₁А - радиус нижнего основания. По условию ОВ= 6√3, О₁А=10√3.
АВ - образующая усечённого конуса. АВ - наклонная к плоскости нижнего основания. Опустим перпендикуляр ВН к плоскости нижнего основания. ВН⊥О₁А. АН - проекция наклонной АВ. Тогда ∠ВАН - угол между наклонной и проекцией наклонной ⇒ ∠ВАН=60°.
ОВАО₁ - прямоугольная трапеция с основаниями ОВ и О₁А, Так как ОО₁⊥О₁А (высота усечённого конуса), и ВН⊥О₁А , а ОВ║О₁А (как радиусы оснований), то ОВНО₁ - прямоугольник ⇒ ОО₁=ВН, а НО₁=ОВ=6√3
АН=О₁А-НО₁=10√3-6√3= 4√3
Рассмотрим прямоугольный треугольник ВНА(∠Н=90°)
∠НВА=90°-∠ВАН=90°-60°=30° - по теореме о сумме углов прямоугольного треугольника.
АН=1/2*АВ - как катет, лежащий против угла 30°, следовательно:
АВ=2*АН=2*4√3= 8√3
По теореме Пифагора находим катет ВН (высоту конуса):
ВН²=АВ²-АН²=(8√3)²-(4√3)²=64·3-16·3=(64-16)·3=48·3=144
Н=ВН= 12 (ед)
2) Отношение площадей боковой и полной поверхности конуса равно 7/8. Найти угол между образующей и плоскостью основания конуса.
Пусть А - центр основания конуса. СА = Н - высота конуса.
В - точка, взятая на окружности основания. Тогда АВ=R - радиус основания конуса. СВ=L - образующая усечённого конуса.
СВ - наклонная к плоскости нижнего основания. Так как СА⊥АВ, то АВ - проекция наклонной СВ. Тогда угол ∠СВА - это угол между наклонной и проекцией наклонной - искомый.
Площадь боковой поверхности конуса:
Sб=πRL
Площадь полной поверхности конуса:
Sп=πR(R+L)
По условию: Sб/Sп=7/8, тогда:
8L=7R+7L
L=7R
Рассмотрим прямоугольный треугольник АВС(∠А=90°)
- Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Поскольку ΔАВС - прямоугольный, то ∠СВА - острый угол.
Тогда ∠СВА=arccos (1/7) или ∠СВА≈82°