Предмет: Математика,
автор: t7f7td7tf
знайти частковий розв'язок диференціального рівняння з розділяючими зміннними
Допоможіть, будь ласка :)
Приложения:
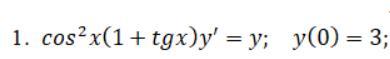
Ответы
Автор ответа:
1
Ответ:
Частное решения дифференциального уравнения с разделяющимися переменными:
Примечание:
Производная через дифференциалы:
Пошаговое объяснение:
Начальные условия:
- общий интеграл дифференциального уравнения
- обще решение
Частное решение:
Похожие вопросы
Предмет: Українська мова,
автор: katerinabaricka
Предмет: История,
автор: rusin0610
Предмет: История,
автор: nastasyaguseva00
Предмет: Английский язык,
автор: redgrapefruit