Question

Розв'яжіть нерівність |3x - 1| * (x - 2) < 0

Answer 1

Ответ:

Объяснение:

|3x - 1| * (x - 2) < 0

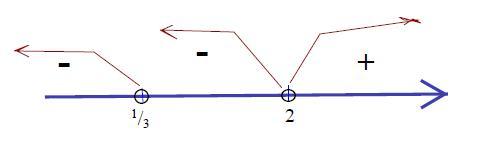
Решаем графически.

Находим х, при которых неравенство = 0:

|3x - 1| * (x - 2) = 0

х₁ = 1/3,  х₂ = 2

В точках, где функция принимает нулевые значения, обычно и происходит смена знака.

При х < 1/3 , например, при х =0 → |-1|*(-3) = -3 < 0

При 1/3 < x < 2 , например, при х = 1 → |3-1|*(-1) = -2 < 0

x > 2,  x = 3 → |3*3-1| *(3-2) = 8 > 0

Т.о. , при х < 1/3  и 1/3 < x < 2 неравенство выполняется, т.е. оно < 0

x ∈ (-∞;1/3) ∪ (1/3; 2)

-------------------

Можно и так: т.к. модуль всегда положителен, то для того, чтобы произведение было отрицательным, второй множитель (х-2) должен быть < 0:

x - 2 < 0 → x < 2

Но надо иметь ввиду, что при х = 1/3 и х =2 выражение = 0.